Note: Unless otherwise indicated, the values for Young’s modulus Y, the shear modulus S, and the bulk modulus B are given, respectively, in Table 10.1, Table 10.2, and Table 10.3.
Section 10.1 The Ideal Spring and Simple Harmonic Motion
|
A hand exerciser utilizes a coiled spring. A force of 89.0 N is required to compress the spring by 0.0191 m. Determine the force needed to compress the spring by 0.0508 m.
|  | |
When the rubber band in a slingshot is stretched, it obeys Hooke’s law. Suppose that the “spring constant” for the rubber band is k =
= 44 N/m. When the rubber band is pulled back with a force of 9.6 N, how far does it stretch?
44 N/m. When the rubber band is pulled back with a force of 9.6 N, how far does it stretch?
The graph shows the force F that an archer applies to the string of a long bow versus the string’s displacement x. Drawing back this bow is analogous to stretching a spring. From the data in the graph determine the effective spring constant of the bow.
|
A car is hauling a 92-kg trailer, to which it is connected by a spring. The spring constant is 2300 N/m. The car accelerates with an acceleration of 0.30 m/s2. By how much does the spring stretch?
|  | |
A 0.70-kg block is hung from and stretches a spring that is attached to the ceiling. A second block is attached to the first one, and the amount that the spring stretches from its unstrained length triples. What is the mass of the second block?
|
A small ball is attached to one end of a spring that has an unstrained length of 0.200 m. The spring is held by the other end, and the ball is whirled around in a horizontal circle at a speed of 3.00 m/s. The spring remains nearly parallel to the ground during the motion and is observed to stretch by 0.010 m. By how much would the spring stretch if it were attached to the ceiling and the ball allowed to hang straight down, motionless?
|  | |
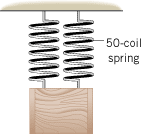
Review Conceptual Example 2 as an aid in solving this problem. An object is attached to the lower end of a 100-coil spring that is hanging from the ceiling. The spring stretches by 0.160 m. The spring is then cut into two identical springs of 50 coils each. As the drawing shows, each spring is attached between the ceiling and the object. By how much does each spring stretch?
|
A 10.1-kg uniform board is wedged into a corner and held by a spring at a 50.0° angle, as the drawing shows. The spring has a spring constant of 176 N/m and is parallel to the floor. Find the amount by which the spring is stretched from its unstrained length.
|  | |
|
In 0.750 s, a 7.00-kg block is pulled through a distance of 4.00 m on a frictionless horizontal surface, starting from rest. The block has a constant acceleration and is pulled by means of a horizontal spring that is attached to the block. The spring constant of the spring is 415 N/m. By how much does the spring stretch?
|  | |
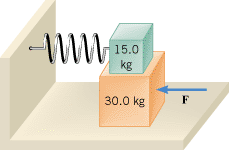
A 30.0-kg block is resting on a flat horizontal table. On top of this block is resting a 15.0-kg block, to which a horizontal spring is attached, as the drawing illustrates. The spring constant of the spring is 325 N/m. The coefficient of kinetic friction between the lower block and the table is 0.600, and the coefficient of static friction between the two blocks is 0.900. A horizontal force F is applied to the lower block as shown. This force is increasing in such a way as to keep the blocks moving at a constant speed. At the point where the upper block begins to slip on the lower block, determine (a) the amount by which the spring is compressed and (b) the magnitude of the force F.
 |
|
A 15.0-kg block rests on a horizontal table and is attached to one end of a massless, horizontal spring. By pulling horizontally on the other end of the spring, someone causes the block to accelerate uniformly and reach a speed of 5.00 m/s in 0.500 s. In the process, the spring is stretched by 0.200 m. The block is then pulled at a constant speed of 5.00 m/s, during which time the spring is stretched by only 0.0500 m. Find (a) the spring constant of the spring and (b) the coefficient of kinetic friction between the block and the table.
|  | |
Section 10.2 Simple Harmonic Motion and the Reference Circle
A loudspeaker diaphragm is producing a sound for 2.5 s by moving back and forth in simple harmonic motion. The angular frequency of the motion is 7.54 ×
× 104 rad/s. How many times does the diaphragm move back and forth?
104 rad/s. How many times does the diaphragm move back and forth?
|
The shock absorbers in the suspension system of a car are in such bad shape that they have no effect on the behavior of the springs attached to the axles. Each of the identical springs attached to the front axle supports 320 kg. A person pushes down on the middle of the front end of the car and notices that it vibrates through five cycles in 3.0 s. Find the spring constant of either spring.
|  | |
Refer to Conceptual Example 2 as an aid in solving this problem. A 100-coil spring has a spring constant of 420 N/m. It is cut into four shorter springs, each of which has 25 coils. One end of a 25-coil spring is attached to a wall. An object of mass 46 kg is attached to the other end of the spring, and the system is set into horizontal oscillation. What is the angular frequency of the motion?
A computer to be used in a satellite must be able to withstand accelerations of up to 25 times the acceleration due to gravity. In a test to see whether it meets this specification, the computer is bolted to a frame that is vibrated back and forth in simple harmonic motion at a frequency of 9.5 Hz. What is the minimum amplitude of vibration that must be used in this test?
|
Objects of equal mass are oscillating up and down in simple harmonic motion on two different vertical springs. The spring constant of spring 1 is 174 N/m. The motion of the object on spring 1 has twice the amplitude as the motion of the object on spring 2. The magnitude of the maximum velocity is the same in each case. Find the spring constant of spring 2.
|  | |
When an object of mass m1 is hung on a vertical spring and set into vertical simple harmonic motion, its frequency is 12.0 Hz. When another object of mass m2 is hung on the spring along with m1, the frequency of the motion is 4.00 Hz. Find the ratio m2/m1 of the masses.
|
Interactive LearningWare 10.1 reviews the concepts involved in this problem. A spring stretches by 0.018 m when a 2.8-kg object is suspended from its end. How much mass should be attached to this spring so that its frequency of vibration is f = = 3.0 Hz? 3.0 Hz?
|  | |
A 3.0-kg block is placed between two horizontal springs. Neither spring is strained when the block is located at the position labeled x =
= 0 m in the drawing. The block is then displaced a distance of 0.070 m from the position where x
0 m in the drawing. The block is then displaced a distance of 0.070 m from the position where x =
= 0 m and released from rest. (a) What is the speed of the block when it passes back through the x
0 m and released from rest. (a) What is the speed of the block when it passes back through the x =
= 0 m position? (b) Determine the angular frequency w of this system.
0 m position? (b) Determine the angular frequency w of this system.
Section 10.3 Energy and Simple Harmonic Motion
An archer pulls the bowstring back for a distance of 0.470 m before releasing the arrow. The bow and string act like a spring whose spring constant is 425 N/m. (a) What is the elastic potential energy of the drawn bow? (b) The arrow has a mass of 0.0300 kg. How fast is it traveling when it leaves the bow?
|
Concept Simulation 10.1 allows you to explore the concepts to which this problem relates. A 2.00-kg object is hanging from the end of a vertical spring. The spring constant is 50.0 N/m. The object is pulled 0.200 m downward and released from rest. Complete the table below by calculating the translational kinetic energy, the gravitational potential energy, the elastic potential energy, and the total mechanical energy E for each of the vertical positions indicated. The vertical positions h indicate distances above the point of release, where h = = 0 m. 0 m.
h (meters)
|
KE
|
PE (gravity)
|
PE (elastic)
|
E
| |
0
|
|
|
|
|
0.200
|
|
|
|
|
0.400
|
|
|
|
|
|
|  | |
In preparation for shooting a ball in a pinball machine, a spring (k =
= 675 N/m) is compressed by 0.0650 m relative to its unstrained length. The ball (m
675 N/m) is compressed by 0.0650 m relative to its unstrained length. The ball (m =
= 0.0585 kg) is at rest against the spring at point A. When the spring is released, the ball slides (without rolling) to point B, which is 0.300 m higher than point A. How fast is the ball moving at B?
0.0585 kg) is at rest against the spring at point A. When the spring is released, the ball slides (without rolling) to point B, which is 0.300 m higher than point A. How fast is the ball moving at B?
|
A spring is hung from the ceiling. A 0.450-kg block is then attached to the free end of the spring. When released from rest, the block drops 0.150 m before momentarily coming to rest. (a) What is the spring constant of the spring? (b) Find the angular frequency of the block’s vibrations.
|  | |
A vertical spring with a spring constant of 450 N/m is mounted on the floor. From directly above the spring, which is unstrained, a 0.30-kg block is dropped from rest. It collides with and sticks to the spring, which is compressed by 2.5 cm in bringing the block to a momentary halt. Assuming air resistance is negligible, from what height (in cm) above the compressed spring was the block dropped?
|
A 1.00 × × 10–2-kg block is resting on a horizontal frictionless surface and is attached to a horizontal spring whose spring constant is 124 N/m. The block is shoved parallel to the spring axis and is given an initial speed of 8.00 m/s, while the spring is initially unstrained. What is the amplitude of the resulting simple harmonic motion? 10–2-kg block is resting on a horizontal frictionless surface and is attached to a horizontal spring whose spring constant is 124 N/m. The block is shoved parallel to the spring axis and is given an initial speed of 8.00 m/s, while the spring is initially unstrained. What is the amplitude of the resulting simple harmonic motion?
|  | |
A 3.2-kg block is hanging stationary from the end of a vertical spring that is attached to the ceiling. The elastic potential energy of this spring/mass system is 1.8 J. What is the elastic potential energy of the system when the 3.2-kg block is replaced by a 5.0-kg block?
Review Conceptual Example 8 before starting this problem. A block is attached to a horizontal spring and oscillates back and forth on a frictionless horizontal surface at a frequency of 3.00 Hz. The amplitude of the motion is 5.08 ×
× 10–2 m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. (a) What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits? (b) Repeat part (a), assuming that the block splits when it is at one of its extreme positions.
10–2 m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. (a) What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits? (b) Repeat part (a), assuming that the block splits when it is at one of its extreme positions.
|
A 1.1-kg object is suspended from a vertical spring whose spring constant is 120 N/m. (a) Find the amount by which the spring is stretched from its unstrained length. (b) The object is pulled straight down by an additional distance of 0.20 m and released from rest. Find the speed with which the object passes through its original position on the way up.
<workedSolution></workedSolution>
|  | |
An 86.0-kg climber is scaling the vertical wall of a mountain. His safety rope is made of nylon that, when stretched, behaves like a spring with a spring constant of 1.20 ×
× 103 N/m. He accidentally slips and falls freely for 0.750 m before the rope runs out of slack. How much is the rope stretched when it breaks his fall and momentarily brings him to rest?
103 N/m. He accidentally slips and falls freely for 0.750 m before the rope runs out of slack. How much is the rope stretched when it breaks his fall and momentarily brings him to rest?
A 1.00 ×
× 10–2-kg bullet is fired horizontally into a 2.50-kg wooden block attached to one end of a massless, horizontal spring (k
10–2-kg bullet is fired horizontally into a 2.50-kg wooden block attached to one end of a massless, horizontal spring (k =
= 845 N/m). The other end of the spring is fixed in place, and the spring is unstrained initially. The block rests on a horizontal, frictionless surface. The bullet strikes the block perpendicularly and quickly comes to a halt within it. As a result of this completely inelastic collision, the spring is compressed along its axis and causes the block/bullet to oscillate with an amplitude of 0.200 m. What is the speed of the bullet?
845 N/m). The other end of the spring is fixed in place, and the spring is unstrained initially. The block rests on a horizontal, frictionless surface. The bullet strikes the block perpendicularly and quickly comes to a halt within it. As a result of this completely inelastic collision, the spring is compressed along its axis and causes the block/bullet to oscillate with an amplitude of 0.200 m. What is the speed of the bullet?
|
A 70.0-kg circus performer is fired from a cannon that is elevated at an angle of 40.0° above the horizontal. The cannon uses strong elastic bands to propel the performer, much in the same way that a slingshot fires a stone. Setting up for this stunt involves stretching the bands by 3.00 m from their unstrained length. At the point where the performer flies free of the bands, his height above the floor is the same as that of the net into which he is shot. He takes 2.14 s to travel the horizontal distance of 26.8 m between this point and the net. Ignore friction and air resistance and determine the effective spring constant of the firing mechanism.
|  | |
Interactive LearningWare 10.2 explores the approach taken in problems such as this one. A spring is mounted vertically on the floor. The mass of the spring is negligible. A certain object is placed on the spring to compress it. When the object is pushed further down by just a bit and then released, one up/down oscillation cycle occurs in 0.250 s. However, when the object is pushed down by 5.00 ×
× 10–2 m to point P and then released, the object flies entirely off the spring. To what height above point P does the object rise in the absence of air resistance?
10–2 m to point P and then released, the object flies entirely off the spring. To what height above point P does the object rise in the absence of air resistance?
Section 10.4 The Pendulum
|
If the period of a simple pendulum is to be 2.0 s, what should be its length?
|  | |
A simple pendulum is made from a 0.65-m-long string and a small ball attached to its free end. The ball is pulled to one side through a small angle and then released from rest. After the ball is released, how much time elapses before it attains its greatest speed?
|
Concept Simulation 10.2 allows you to explore the effect of the acceleration due to gravity on pendulum motion, which is the focus of this problem. Astronauts on a distant planet set up a simple pendulum of length 1.2 m. The pendulum executes simple harmonic motion and makes 100 complete vibrations in 280 s. What is the acceleration due to gravity?
|  | |
A pendulum clock can be approximated as a simple pendulum of length 1.00 m and keeps accurate time at a location where g =
= 9.83 m/s2. In a location where g
9.83 m/s2. In a location where g =
= 9.78 m/s2, what must be the new length of the pendulum, such that the clock continues to keep accurate time (that is, its period remains the same)?
9.78 m/s2, what must be the new length of the pendulum, such that the clock continues to keep accurate time (that is, its period remains the same)?
|
Pendulum A is a physical pendulum made from a thin, rigid, and uniform rod whose length is d. One end of this rod is attached to the ceiling by a frictionless hinge, so the rod is free to swing back and forth. Pendulum B is a simple pendulum whose length is also d. Obtain the ratio TA/TB of their periods for small-angle oscillations.
|  | |
A pendulum is constructed from a thin, rigid, and uniform rod with a small sphere attached to the end opposite the pivot. This arrangement is a good approximation to a simple pendulum (period =
= 0.66 s), because the mass of the sphere (lead) is much greater than the mass of the rod (aluminum). When the sphere is removed, the pendulum no longer is a simple pendulum, but is then a physical pendulum. What is the period of the physical pendulum?
0.66 s), because the mass of the sphere (lead) is much greater than the mass of the rod (aluminum). When the sphere is removed, the pendulum no longer is a simple pendulum, but is then a physical pendulum. What is the period of the physical pendulum?
Section 10.7 Elastic Deformation, Section 10.8 Stress, Strain, and Hooke’s Law
A tow truck is pulling a car out of a ditch by means of a steel cable that is 9.1 m long and has a radius of 0.50 cm. When the car just begins to move, the tension in the cable is 890 N. How much has the cable stretched?
A copper cube, 0.30 m on a side, is subjected to two shearing forces, each of magnitude F =
= 6.0
6.0 ×
× 106 N (see the drawing). Find the angle q (in degrees), which is one measure of how the shape of the block has been altered by shear deformation.
106 N (see the drawing). Find the angle q (in degrees), which is one measure of how the shape of the block has been altered by shear deformation.
An 1800-kg car, being lifted at a steady speed by a crane, hangs at the end of a cable whose radius is 6.0 ×
× 10–3 m. The cable is 15 m in length and stretches by 8.0
10–3 m. The cable is 15 m in length and stretches by 8.0 ×
× 10–3 m because of the weight of the car. Determine (a) the stress, (b) the strain, and (c) Young’s modulus for the cable.
10–3 m because of the weight of the car. Determine (a) the stress, (b) the strain, and (c) Young’s modulus for the cable.
The femur is a bone in the leg whose minimum cross-sectional area is about 4.0 ×
× 10–4 m2. A compressional force in excess of 6.8
10–4 m2. A compressional force in excess of 6.8 ×
× 104 N will fracture this bone. (a) Find the maximum stress that this bone can withstand. (b) What is the strain that exists under a maximum-stress condition?
104 N will fracture this bone. (a) Find the maximum stress that this bone can withstand. (b) What is the strain that exists under a maximum-stress condition?
|
A piece of aluminum is surrounded by air at a pressure of 1.01 × × 105 Pa. The aluminum is placed in a vacuum chamber where the pressure is reduced to zero. Determine the fractional change DV/V0 in the volume of the aluminum. 105 Pa. The aluminum is placed in a vacuum chamber where the pressure is reduced to zero. Determine the fractional change DV/V0 in the volume of the aluminum.
|  | |
When subjected to a force of compression, the length of a bone decreases by 2.7 ×
× 10–5 m. When this same bone is subjected to a tensile force of the same magnitude, by how much does it stretch?
10–5 m. When this same bone is subjected to a tensile force of the same magnitude, by how much does it stretch?
A copper cylinder and a brass cylinder are stacked end to end, as in the drawing. Each cylinder has a radius of 0.25 cm. A compressive force of F =
= 6500 N is applied to the right end of the brass cylinder. Find the amount by which the length of the stack decreases.
6500 N is applied to the right end of the brass cylinder. Find the amount by which the length of the stack decreases.
A gymnast does a one-arm handstand. The humerus, which is the upper arm bone between the elbow and the shoulder joint, may be approximated as a 0.30-m-long cylinder with an outer radius of 1.00 ×
× 10–2 m and a hollow inner core with a radius of 4.0
10–2 m and a hollow inner core with a radius of 4.0 ×
× 10–3 m. Excluding the arm, the mass of the gymnast is 63 kg. (a) What is the compressional strain of the humerus? (b) By how much is the humerus compressed?
10–3 m. Excluding the arm, the mass of the gymnast is 63 kg. (a) What is the compressional strain of the humerus? (b) By how much is the humerus compressed?
|
A helicopter is lifting a 2100-kg jeep. The steel suspension cable is 48 m long and has a radius of 5.0 × × 10–3 m. (a) Find the amount that the cable is stretched when the jeep is suspended motionless in the air. (b) What is the amount of cable stretch when the jeep is hoisted upward with an acceleration of 1.5 m/s2? 10–3 m. (a) Find the amount that the cable is stretched when the jeep is suspended motionless in the air. (b) What is the amount of cable stretch when the jeep is hoisted upward with an acceleration of 1.5 m/s2?
|  | |
A block of copper is securely fastened to the floor. A force of 1800 N is applied to the top surface of the block, as the drawing shows. Find (a) the amount by which the height of the block is changed and (b) the shear deformation of the block.
|
An 8.0-kg stone at the end of a steel wire is being whirled in a circle at a constant tangential speed of 12 m/s. The stone is moving on the surface of a frictionless horizontal table. The wire is 4.0 m long and has a radius of 1.0 × × 10–3 m. Find the strain in the wire. 10–3 m. Find the strain in the wire.
|  | |
Two rods are identical in all respects except one: one rod is made from aluminum, and the other from tungsten. The rods are joined end to end, in order to make a single rod that is twice as long as either the aluminum or tungsten rod. What is the effective value of Young’s modulus for this composite rod? That is, what value YComposite of Young’s modulus should be used in Equation 10.17 when applied to the composite rod? Note that the change DLComposite in the length of the composite rod is the sum of the changes in length of the aluminum and tungsten rods.
A square plate is 1.0 ×
× 10–2 m thick, measures 3.0
10–2 m thick, measures 3.0 ×
× 10–2 m on a side, and has a mass of 7.2
10–2 m on a side, and has a mass of 7.2 ×
× 10–2 kg. The shear modulus of the material is 2.0
10–2 kg. The shear modulus of the material is 2.0 ×
× 1010 N/m2. One of the square faces rests on a flat horizontal surface, and the coefficient of static friction between the plate and the surface is 0.90. A force is applied to the top of the plate, as in Figure 10.31a. Determine (a) the maximum possible amount of shear stress, (b) the maximum possible amount of shear strain, and (c) the maximum possible amount of shear deformation DX (see Figure 10.31b) that can be created by the applied force just before the plate begins to move.
1010 N/m2. One of the square faces rests on a flat horizontal surface, and the coefficient of static friction between the plate and the surface is 0.90. A force is applied to the top of the plate, as in Figure 10.31a. Determine (a) the maximum possible amount of shear stress, (b) the maximum possible amount of shear strain, and (c) the maximum possible amount of shear deformation DX (see Figure 10.31b) that can be created by the applied force just before the plate begins to move.
A cylindrically shaped piece of collagen (a substance found in the body in connective tissue) is being stretched by a force that increases from 0 to 3.0 ×
× 10–2 N. The length and radius of the collagen are, respectively, 2.5 and 0.091 cm, and Young’s modulus is 3.1
10–2 N. The length and radius of the collagen are, respectively, 2.5 and 0.091 cm, and Young’s modulus is 3.1 ×
× 106 N/m2. (a) If the stretching obeys Hooke’s law, what is the spring constant k for collagen? (b) How much work is done by the variable force that stretches the collagen? (See Section 6.9 for a discussion of the work done by a variable force.)
106 N/m2. (a) If the stretching obeys Hooke’s law, what is the spring constant k for collagen? (b) How much work is done by the variable force that stretches the collagen? (See Section 6.9 for a discussion of the work done by a variable force.)
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() =
=![]() 44 N/m. When the rubber band is pulled back with a force of 9.6 N, how far does it stretch?
44 N/m. When the rubber band is pulled back with a force of 9.6 N, how far does it stretch?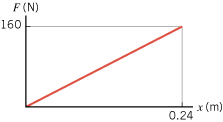

![]() ×
×![]() 104 rad/s. How many times does the diaphragm move back and forth?
104 rad/s. How many times does the diaphragm move back and forth?![]() =
=![]() 0 m in the drawing. The block is then displaced a distance of 0.070 m from the position where x
0 m in the drawing. The block is then displaced a distance of 0.070 m from the position where x![]() =
=![]() 0 m and released from rest. (a) What is the speed of the block when it passes back through the x
0 m and released from rest. (a) What is the speed of the block when it passes back through the x![]() =
=![]() 0 m position? (b) Determine the angular frequency w of this system.
0 m position? (b) Determine the angular frequency w of this system.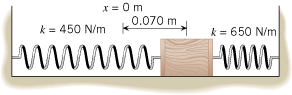
![]() =
=![]() 675 N/m) is compressed by 0.0650 m relative to its unstrained length. The ball (m
675 N/m) is compressed by 0.0650 m relative to its unstrained length. The ball (m![]() =
=![]() 0.0585 kg) is at rest against the spring at point A. When the spring is released, the ball slides (without rolling) to point B, which is 0.300 m higher than point A. How fast is the ball moving at B?
0.0585 kg) is at rest against the spring at point A. When the spring is released, the ball slides (without rolling) to point B, which is 0.300 m higher than point A. How fast is the ball moving at B?![]() ×
×![]() 10–2 m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. (a) What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits? (b) Repeat part (a), assuming that the block splits when it is at one of its extreme positions.
10–2 m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. (a) What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits? (b) Repeat part (a), assuming that the block splits when it is at one of its extreme positions.![]() ×
×![]() 103 N/m. He accidentally slips and falls freely for 0.750 m before the rope runs out of slack. How much is the rope stretched when it breaks his fall and momentarily brings him to rest?
103 N/m. He accidentally slips and falls freely for 0.750 m before the rope runs out of slack. How much is the rope stretched when it breaks his fall and momentarily brings him to rest?![]() ×
×![]() 10–2-kg bullet is fired horizontally into a 2.50-kg wooden block attached to one end of a massless, horizontal spring (k
10–2-kg bullet is fired horizontally into a 2.50-kg wooden block attached to one end of a massless, horizontal spring (k![]() =
=![]() 845 N/m). The other end of the spring is fixed in place, and the spring is unstrained initially. The block rests on a horizontal, frictionless surface. The bullet strikes the block perpendicularly and quickly comes to a halt within it. As a result of this completely inelastic collision, the spring is compressed along its axis and causes the block/bullet to oscillate with an amplitude of 0.200 m. What is the speed of the bullet?
845 N/m). The other end of the spring is fixed in place, and the spring is unstrained initially. The block rests on a horizontal, frictionless surface. The bullet strikes the block perpendicularly and quickly comes to a halt within it. As a result of this completely inelastic collision, the spring is compressed along its axis and causes the block/bullet to oscillate with an amplitude of 0.200 m. What is the speed of the bullet?![]() ×
×![]() 10–2 m to point P and then released, the object flies entirely off the spring. To what height above point P does the object rise in the absence of air resistance?
10–2 m to point P and then released, the object flies entirely off the spring. To what height above point P does the object rise in the absence of air resistance?![]() =
=![]() 9.83 m/s2. In a location where g
9.83 m/s2. In a location where g![]() =
=![]() 9.78 m/s2, what must be the new length of the pendulum, such that the clock continues to keep accurate time (that is, its period remains the same)?
9.78 m/s2, what must be the new length of the pendulum, such that the clock continues to keep accurate time (that is, its period remains the same)?![]() =
=![]() 0.66 s), because the mass of the sphere (lead) is much greater than the mass of the rod (aluminum). When the sphere is removed, the pendulum no longer is a simple pendulum, but is then a physical pendulum. What is the period of the physical pendulum?
0.66 s), because the mass of the sphere (lead) is much greater than the mass of the rod (aluminum). When the sphere is removed, the pendulum no longer is a simple pendulum, but is then a physical pendulum. What is the period of the physical pendulum?![]() =
=![]() 6.0
6.0![]() ×
×![]() 106 N (see the drawing). Find the angle q (in degrees), which is one measure of how the shape of the block has been altered by shear deformation.
106 N (see the drawing). Find the angle q (in degrees), which is one measure of how the shape of the block has been altered by shear deformation.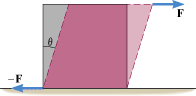
![]() ×
×![]() 10–3 m. The cable is 15 m in length and stretches by 8.0
10–3 m. The cable is 15 m in length and stretches by 8.0![]() ×
×![]() 10–3 m because of the weight of the car. Determine (a) the stress, (b) the strain, and (c) Young’s modulus for the cable.
10–3 m because of the weight of the car. Determine (a) the stress, (b) the strain, and (c) Young’s modulus for the cable.![]() ×
×![]() 10–4 m2. A compressional force in excess of 6.8
10–4 m2. A compressional force in excess of 6.8![]() ×
×![]() 104 N will fracture this bone. (a) Find the maximum stress that this bone can withstand. (b) What is the strain that exists under a maximum-stress condition?
104 N will fracture this bone. (a) Find the maximum stress that this bone can withstand. (b) What is the strain that exists under a maximum-stress condition?![]() ×
×![]() 10–5 m. When this same bone is subjected to a tensile force of the same magnitude, by how much does it stretch?
10–5 m. When this same bone is subjected to a tensile force of the same magnitude, by how much does it stretch?![]() =
=![]() 6500 N is applied to the right end of the brass cylinder. Find the amount by which the length of the stack decreases.
6500 N is applied to the right end of the brass cylinder. Find the amount by which the length of the stack decreases.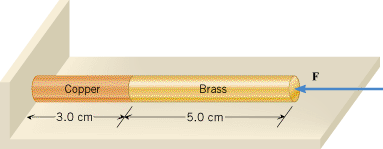
![]() ×
×![]() 10–2 m and a hollow inner core with a radius of 4.0
10–2 m and a hollow inner core with a radius of 4.0![]() ×
×![]() 10–3 m. Excluding the arm, the mass of the gymnast is 63 kg. (a) What is the compressional strain of the humerus? (b) By how much is the humerus compressed?
10–3 m. Excluding the arm, the mass of the gymnast is 63 kg. (a) What is the compressional strain of the humerus? (b) By how much is the humerus compressed?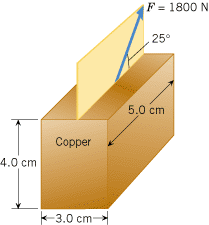
![]() ×
×![]() 10–2 m thick, measures 3.0
10–2 m thick, measures 3.0![]() ×
×![]() 10–2 m on a side, and has a mass of 7.2
10–2 m on a side, and has a mass of 7.2![]() ×
×![]() 10–2 kg. The shear modulus of the material is 2.0
10–2 kg. The shear modulus of the material is 2.0![]() ×
×![]() 1010 N/m2. One of the square faces rests on a flat horizontal surface, and the coefficient of static friction between the plate and the surface is 0.90. A force is applied to the top of the plate, as in Figure 10.31a. Determine (a) the maximum possible amount of shear stress, (b) the maximum possible amount of shear strain, and (c) the maximum possible amount of shear deformation DX (see Figure 10.31b) that can be created by the applied force just before the plate begins to move.
1010 N/m2. One of the square faces rests on a flat horizontal surface, and the coefficient of static friction between the plate and the surface is 0.90. A force is applied to the top of the plate, as in Figure 10.31a. Determine (a) the maximum possible amount of shear stress, (b) the maximum possible amount of shear strain, and (c) the maximum possible amount of shear deformation DX (see Figure 10.31b) that can be created by the applied force just before the plate begins to move.![]() ×
×![]() 10–2 N. The length and radius of the collagen are, respectively, 2.5 and 0.091 cm, and Young’s modulus is 3.1
10–2 N. The length and radius of the collagen are, respectively, 2.5 and 0.091 cm, and Young’s modulus is 3.1![]() ×
×![]() 106 N/m2. (a) If the stretching obeys Hooke’s law, what is the spring constant k for collagen? (b) How much work is done by the variable force that stretches the collagen? (See Section 6.9 for a discussion of the work done by a variable force.)
106 N/m2. (a) If the stretching obeys Hooke’s law, what is the spring constant k for collagen? (b) How much work is done by the variable force that stretches the collagen? (See Section 6.9 for a discussion of the work done by a variable force.)