18.9.
Gauss' Law
Gauss' law relates the electric flux through a closed surface to the net charge enclosed by the surface. In order to fully understand Gauss' law, we must first discuss the concept of electric flux.
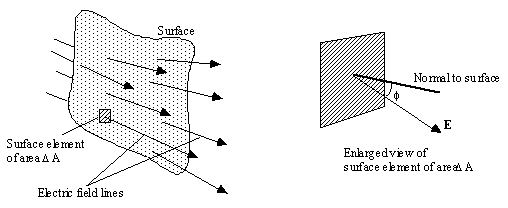
Consider a surface in the vicinity of an electric field as shown in part (a) of the figure below. Imagine dividing the surface into a number of smaller surface elements, each of area
DA. The size of each element is chosen so that the magnitude and direction of the electric field is constant over each surface element. We now imagine constructing the line that is normal to each surface element. In general, the electric field at any point on the surface element will make an angle f with the normal, as shown in part (b) of the figure below.
The electric flux through the entire surface is defined as
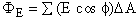 | (18.6) |  |
where E is the magnitude of the electric field at a point on the surface, and f is the angle between the electric field and the normal at that point. The summation is carried out over the entire surface; in other words, the quantity (E cos f)DA is summed for all surface elements that comprise the surface.In general, surfaces can be open or closed. An open surface always has an edge, a rim, or some boundary. Examples include a sheet of paper, a lamp shade, and half of an egg shell. Closed surfaces, on the other hand, do not possess an edge or boundary. Examples of closed surfaces include a sphere and an unbroken egg shell. Gauss's law pertains only to closed surfaces, appropriately named Gaussian surfaces. Clearly, the surface elements on a closed surface have both an inward and an outward normal. In applying Equation (18.6) to closed surfaces, the angle f is, by convention, the angle that the electric field makes with the outward normal. The electric flux through a closed surface will be positive if the electric field lines leave the surface and negative if the electric field lines enter the surface.
Gauss' law states that the electric flux
F
E
through a Gaussian surface is equal to the net charge Q enclosed by the surface divided by
e
0, the permittivity of free space:
 | (18.7) |  |
From Equation (18.7), we see that the flux through a closed surface is positive if it encloses a net positive charge, and negative if the surface encloses a net negative charge.
Gauss's law is an important calculational tool in many circumstances:
| 1. |
It can be used to determine the electric flux through a closed surface without performing the summation in Equation (18.6) if the net enclosed charge Q is known.
|
| 2. |
It can be used to determine the net charge within a closed surface, if the flux through the surface is known (or can be determined).
|
| 3. |
It can be used to determine the magnitude of the electric field for charge distributions that possess a high degree of spatial symmetry.
|
The next two examples illustrate the first two circumstances described above.
Example 6
A point charge of + 5.0 mC is placed at the center of a cube of side length 0.25 m. Determine the electric flux through the cube.
From Gauss' law
While this problem can be solved using Equation (18.6), the method is tedious and requires the use of integral calculus. Gauss' law provides a quick and convenient method that requires only simple arithmetic. Notice that the answer does not depend on the fact that the charge is at the center of the cube. In fact, the electric flux through the cube will be the same regardless of the position of the charge as long as it remains inside the cube. Certainly, if the charge is moved to a different position in the cube, the magnitude of the electric field at points on the surface of the cube will change; however, Gauss' law predicts that the electric field will change in such a way that the flux through the cube remains the same.
Example 7
One day, the electric field in the atmosphere near ground level is 110 N/C. Assume that the magnitude of this field is the same everywhere around the earth and that the direction of the field is radially inward. The radius of the earth is 6.38 × 106 m. Calculate the net charge (magnitude and sign) on the earth.
For the purposes of this problem, imagine that the earth is just surrounded by a spherical Gaussian surface (i.e., the radius of the Gaussian surface is essentially the same as that of the earth). The electric flux through the Gaussian surface is given by
|
F
E = S(E cos f)DA |  |
where f is the angle between the electric field and the outward normal to the surface element
DA. Combining this with Gauss' law, we have
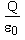 = S(E cos f)DA. = S(E cos f)DA. |  |
Since the electric field is uniform in magnitude and directed radially inward, the angle between the electric field and the outward normal is 180° for each surface element
DA. Furthermore, since the electric field is uniform in magnitude, E can be factored out of the summation. The sum
SDA must equal the surface area of the spherical Gaussian surface. Solving for Q gives
As described above, Gauss' law can also be used to calculate the magnitude of the electric field in the vicinity of a charge distribution provided that the charge distribution (and hence the electric field) possesses sufficient symmetry. The symmetry of the charge distribution is the key factor. Imagine that we surround a point charge with an arbitrarily shaped Gaussian surface. We can deduce from Example 6 that the flux through this surface is the same regardless of its shape; however, we cannot, in general, use Gauss' law to solve for the electric field on the Gaussian surface. For an arbitrarily shaped Gaussian surface, the magnitude of the electric field will, in general, vary from point to point on the surface. Hence, we cannot solve for E in Equation (18.7). In order to solve for E, we must be able to "factor" the E out of the summation. This can only be done if the magnitude of E is constant over the Gaussian surface.
We must then use the symmetry of the charge distribution as a guide in constructing a Gaussian surface over which E is constant. For a charge distribution that possesses spherical symmetry, we can deduce that the magnitude of the electric field should be the same at all points equidistant from the distribution. Therefore, if we surround such a distribution with a spherical Gaussian surface that is concentric with the distribution, we can assume that E is constant on the surface. For a line of charge, we can deduce that the magnitude of the electric field should be the same at all points equidistant from the line of charge. In this case, such points would lie on the surface of a cylinder that is concentric with the line of charge; hence we would construct a cylindrical Gaussian surface.
Example 8
A solid conducting sphere of radius R carries a total charge -q uniformly distributed over the surface of the sphere. Determine the magnitude and direction of the electric field for any point at a distance r from the center of the sphere if (a) r > R (i.e., at any point outside the sphere), and (b) r < R (i.e., at any point inside the sphere).
Since we want to find E, we must perform the calculation with a Gaussian surface over which E is constant. We can assume that since the charge distribution possesses spherical symmetry, the magnitude of the electric field (if it exists), should be the same at all points equidistant from the center of the sphere. Thus, in both parts (a) and (b) we will use spherical Gaussian surfaces.
(a) To find the magnitude of the electric field outside the charged sphere, we construct a spherical Gaussian surface of radius r (r > R) concentric with the charged sphere. The flux through this Gaussian surface is
|
F
E = S(E cos f)DA. |  |
Since the charge is spread uniformly over the surface of the sphere, the charge distribution possesses spherical symmetry. Therefore, we expect the electric field to be directed radially. Since the charge is negative, the field is radially inward;
f = 180° for each surface element, and (E cos 180°) = - E. Furthermore, since the charge distribution is uniform, we expect the electric field to be uniform in magnitude over the Gaussian surface. Hence, E can be factored out of the summation.
|
F
E = - S(EDA) = - E(SDA), |  |
where
SDA is the sum of the area elements that make up the Gaussian surface. This sum must equal the surface area of the spherical Gaussian surface or
|
F
E = - E(SDA) = - E(4pr2) |  |
The explicit statement of Gauss' law becomes
- E(4pr2) = 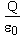 , , |  |
where Q is the net charge enclosed by the Gaussian surface. From the statement of the problem, the net charge Q enclosed by the Gaussian surface is -q. Thus we have
- E(4pr2) = 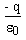 |  |
Solving for E gives
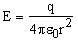 . . |  |
Since the charge is negative the direction of the field must be radially inward. Note that the direction of the electric field is deduced from the fact that the charge is negative. Gauss' law is used only to find the magnitude of the field.
(b) To find the magnitude of the electric field inside the charged sphere, we construct a spherical Gaussian surface of radius r (r < R) concentric with the charged sphere. We can argue, as we did in part (a), that the field (if it exists) should possess spherical symmetry. Using the arguments similar to those of part (a), we find that the explicit statement of Gauss' law for this situation is
E(4pr2) = 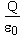 . . |  |
Since we have a conducting sphere, however, all of the charge resides on the outer surface of the sphere. The Gaussian surface encloses zero net charge so Q = 0. Thus we obtain
| E = 0 . |  |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |

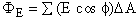

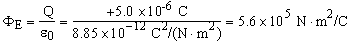
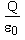 = S(E cos f)DA.
= S(E cos f)DA.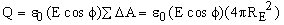
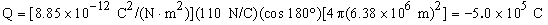
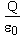 ,
,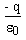
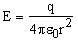 .
.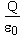 .
.