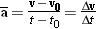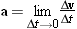3.1.
Displacement, Velocity, and Acceleration
In Chapter 2 the concepts of displacement, velocity, and acceleration are used to describe an object moving in one dimension. There are also situations in which the motion is along a curved path that lies in a plane. Such two-dimensional motion can be described using the same concepts. In Grand Prix racing, for example, the course follows a curved road, and Figure 3.1 shows a race car at two different positions along it. These positions are identified by the vectors r and r0, which are drawn from an arbitrary coordinate origin. The displacement Dr of the car is the vector drawn from the initial position r0 at time t0 to the final position r at time t. The magnitude of Dr is the shortest distance between the two positions. In the drawing, the vectors r0 and Dr are drawn tail to head, so it is evident that r is the vector sum of r0 and Dr. (See Sections 1.5 and 1.6 for a review of vectors and vector addition.) This means that r =
= r0+Dr, or
r0+Dr, or
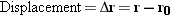 |  |
The displacement here is defined as it is in Chapter 2. Now, however, the displacement vector can lie anywhere in a plane, rather than just along a straight line.
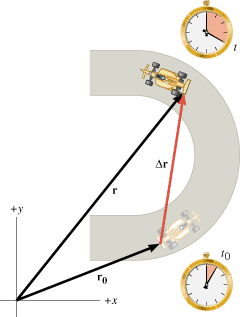 | | Figure 3.1
The displacement D
r of the car is a vector that points from the initial position of the car at time t
0 to the final position at time t.The magnitude of D
r is the shortest distance between the two positions. |
|
The average velocity 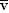 of the car between two positions is defined in a manner similar to that in Equation 2.2, as the displacement Dr
of the car between two positions is defined in a manner similar to that in Equation 2.2, as the displacement Dr =
= r
r –
– r0 divided by the elapsed time Dt
r0 divided by the elapsed time Dt =
= t
t –
– t0:
t0:
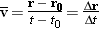 | (3.1) |  |
Since both sides of Equation 3.1 must agree in direction, the average velocity vector has the same direction as the displacement. The velocity of the car at an instant of time is its instantaneous velocity v. The average velocity becomes equal to the instantaneous velocity v in the limit that Dt becomes infinitesimally small:
Figure 3.2 illustrates that the instantaneous velocity v is tangent to the path of the car. The drawing also shows the vector components vx and vy of the velocity, which are parallel to the x and y axes, respectively.
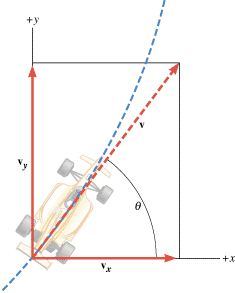 | | Figure 3.2
The instantaneous velocity v and its two vector components v
x
and v
y
.
|
|
| Check Your Understanding 1 |
 |
|
Suppose you are driving due east, traveling a distance of 1500 meters in 2 minutes. You then turn due north and travel the same distance in the same time. What can be said about the average speeds and the average velocities for the two segments of the trip? (a) The average speeds are the same, and the average velocities are the same. (b) The average speeds are the same, but the average velocities are different. (c) The average speeds are different, but the average velocities are the same.
Background:
This question deals with the concepts of velocity (a vector) and speed (a scalar). Think about the additional information conveyed by a vector.
For similar questions (including calculational counterparts), consult Self-Assessment Test 3.1. This test is described at the end of Section 3.3.
|
|
 |
The average acceleration 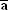 is defined just as it is for one-dimensional motion—namely, as the change in velocity, Dv
is defined just as it is for one-dimensional motion—namely, as the change in velocity, Dv =
= v–v0, divided by the elapsed time Dt:
v–v0, divided by the elapsed time Dt:
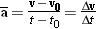 | (3.2) |  |
The average acceleration vector has the same direction as the change in velocity. In the limit that the elapsed time becomes infinitesimally small, the average acceleration becomes equal to the instantaneous acceleration a:
The acceleration has a vector component ax along the x direction and a vector component ay along the y direction.
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() =
=![]() r0+Dr, or
r0+Dr, or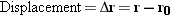

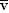 of the car between two positions is defined in a manner similar to that in Equation 2.2, as the displacement Dr
of the car between two positions is defined in a manner similar to that in Equation 2.2, as the displacement Dr![]() =
=![]() r
r![]() –
–![]() r0 divided by the elapsed time Dt
r0 divided by the elapsed time Dt![]() =
=![]() t
t![]() –
–![]() t0:
t0: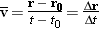
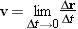

 is defined just as it is for one-dimensional motion—namely, as the change in velocity, Dv
is defined just as it is for one-dimensional motion—namely, as the change in velocity, Dv![]() =
=![]() v–v0, divided by the elapsed time Dt:
v–v0, divided by the elapsed time Dt: