3.2.
Equations of Kinematics in Two Dimensions
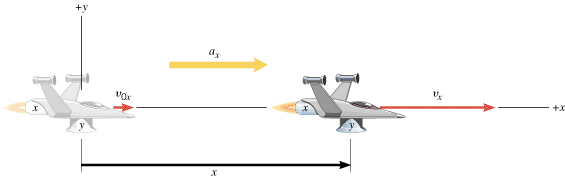 | | Figure 3.3
The spacecraft is moving with a constant acceleration a
x
parallel to the x axis. There is no motion in the y direction, and the y engine is turned off.
|
|
To understand how displacement, velocity, and acceleration are applied to two-dimensional motion, consider a spacecraft equipped with two engines that are mounted perpendicular to each other. These engines produce the only forces that the craft experiences, and the spacecraft is assumed to be at the coordinate origin when t0 =
= 0 s, so that r0
0 s, so that r0 =
= 0 m. At a later time t, the spacecraft’s displacement is Dr
0 m. At a later time t, the spacecraft’s displacement is Dr =
= r–r0
r–r0 =
= r. Relative to the x and y axes, the displacement r has vector components of x and y, respectively.
r. Relative to the x and y axes, the displacement r has vector components of x and y, respectively.
In Figure 3.3 only the engine oriented along the x direction is firing, and the vehicle accelerates along this direction. It is assumed that the velocity in the y direction is zero, and it remains zero, since the y engine is turned off. The motion of the spacecraft along the x direction is described by the five kinematic variables x, ax, vx, v0x, and t. Here the symbol “x” reminds us that we are dealing with the x components of the displacement, velocity, and acceleration vectors. (See Sections 1.7 and 1.8 for a review of vector components.) The variables x, ax, vx, and v0x are scalar components (or “components,” for short). As Section 1.7 discusses, these components are positive or negative numbers (with units), depending on whether the associated vector components point along the +x or the –x axis. If the spacecraft has a constant acceleration along the x direction, the motion is exactly like that described in Chapter 2, and the equations of kinematics can be used. For convenience, these equations are written in the left column of Table 3.1.
 |
 Interactive LearningWare 3.1 Interactive LearningWare 3.1 | A fox runs 85 m due south in 18 s. He starts from rest and stops for a negligible amount of time at the end of the run. Then he takes off again and runs 62 m due east in 21 s. During this second run, his acceleration is constant. For the entire 39-s interval, find the magnitude and direction of the fox’s (a) average velocity and (b) average acceleration. Express the directions relative to due south. Related Homework: Problems 10 |
|
 |
| Table 3.1
Equations of Kinematics for Constant Acceleration Two-Dimensional Motion |
|
x Component
|
Variable
|
y Component
| |
x
|
Displacement
|
y
|
ax
|
Acceleration
|
ay
|
vx
|
Final velocity
|
vy
|
v0x
|
Initial velocity
|
v0y
|
t
|
Elapsed time
|
t
|
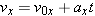 | (3.3a) |  |
|
|
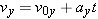 | (3.3b) |  |
|
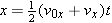 | (3.4a) |  |
|
|
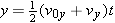 | (3.4b) |  |
|
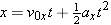 | (3.5a) |  |
|
|
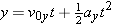 | (3.5b) |  |
|
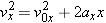 | (3.6a) |  |
|
|
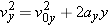 | (3.6b) |  |
|
|
|
Figure 3.4 is analogous to Figure 3.3, except that now only the y engine is firing, and the spacecraft accelerates along the y direction. Such a motion can be described in terms of the kinematic variables y, ay, vy, v0y, and t. And if the acceleration along the y direction is constant, these variables are related by the equations of kinematics, as written in the right column of Table 3.1. Like their counterparts in the x direction, the scalar components, y, ay, vy, and v0y, may be positive (+) or negative (–) numbers (with units).
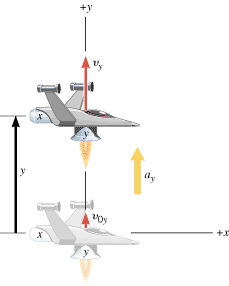 | | Figure 3.4
The spacecraft is moving with a constant acceleration a
y
parallel to the y axis. There is no motion in the x direction, and the x engine is turned off. |
|
If both engines of the spacecraft are firing at the same time, the resulting motion takes place in part along the x axis and in part along the y axis, as Figure 3.5 illustrates. The thrust of each engine gives the vehicle a corresponding acceleration component. The x engine accelerates the ship in the x direction and causes a change in the x component of the velocity. Likewise, the y engine causes a change in the y component of the velocity. It is important to realize that the x part of the motion occurs exactly as it would if the y part did not occur at all. Similarly, the y part of the motion occurs exactly as it would if the x part of the motion did not exist. In other words, the x and y motions are independent of each other.
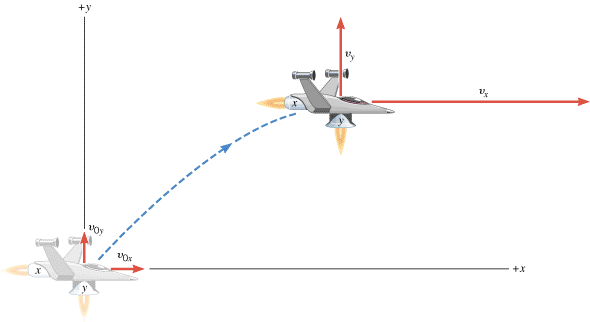 | | Figure 3.5
The two-dimensional motion of the spacecraft can be viewed as the combination of the separate x and y motions. |
|
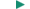 CONCEPTS AT A GLANCE The independence of the x and y motions lies at the heart of two-dimensional kinematics. It allows us to treat two-dimensional motion as two distinct one-dimensional motions, one for the x direction and one for the y direction. As the Concepts-at-a-Glance chart in Figure 3.6 illustrates, everything that we have learned in Chapter 2 about kinematics in one dimension will now be applied separately to each of the two directions. In so doing, we will be able to describe the x and y variables separately and then bring these descriptions together to understand the two-dimensional picture. Example 4 takes this approach in dealing with a moving spacecraft.
CONCEPTS AT A GLANCE The independence of the x and y motions lies at the heart of two-dimensional kinematics. It allows us to treat two-dimensional motion as two distinct one-dimensional motions, one for the x direction and one for the y direction. As the Concepts-at-a-Glance chart in Figure 3.6 illustrates, everything that we have learned in Chapter 2 about kinematics in one dimension will now be applied separately to each of the two directions. In so doing, we will be able to describe the x and y variables separately and then bring these descriptions together to understand the two-dimensional picture. Example 4 takes this approach in dealing with a moving spacecraft.
|
| Figure 3.6
CONCEPTS AT A GLANCE In two dimensions, motion along the x direction and motion along the y direction are independent of each other. As a result, each can be analyzed separately according to the procedures for one-dimensional kinematics discussed in Chapter 2. On the space shuttle Challenger, motion in perpendicular directions is controlled by thrusters. The photographs show the Challenger in orbit with different thrusters activated. (Courtesy NASA). |
|
| Example 1 A Moving Spacecraft |
 |
|
In the x direction, the spacecraft in Figure 3.5 has an initial velocity component of v0x = = +22 m/s and an acceleration component of ax +22 m/s and an acceleration component of ax = = +24 m/s2. In the y direction, the analogous quantities are v0y +24 m/s2. In the y direction, the analogous quantities are v0y = = +14 m/s and ay +14 m/s and ay = = +12 m/s2. The directions to the right and upward have been chosen as the positive directions. Find (a) x and vx, (b) y and vy, and (c) the final velocity (magnitude and direction) of the spacecraft at time t +12 m/s2. The directions to the right and upward have been chosen as the positive directions. Find (a) x and vx, (b) y and vy, and (c) the final velocity (magnitude and direction) of the spacecraft at time t = = 7.0 s. 7.0 s.
Reasoning
The motion in the x direction and the motion in the y direction can be treated separately, each as a one-dimensional motion. We will follow this approach in parts (a) and (b) to obtain the location and velocity components of the spacecraft. Then, in part (c) the velocity components will be combined to give the final velocity.
Problem solving insight
When the motion is two-dimensional, the time variable t has the same value for both the x and y directions. |
|
Solution
| (a) |
The data for the motion in the x direction are listed below.
x-Direction Data
|
x
|
ax
|
vx
|
v0x
|
t
|
?
|
+24 m/s2
|
?
|
+22 m/s
|
7.0 s
|
The x component of the craft’s displacement can be found by using Equation 3.5a.
The velocity component vx can be calculated with the aid of Equation 3.3a:
| | (b) |
The data for the motion in the y direction are listed below.
y-Direction Data
|
y
|
ay
|
vy
|
v0y
|
t
|
?
|
+12 m/s2
|
?
|
+14 m/s
|
7.0 s
|
Proceeding in the same manner as in part (a), we find that
| | (c) |
Figure 3.7 shows the velocity of the vehicle and its components vx and vy. The magnitude v of the velocity can be found by using the Pythagorean theorem:
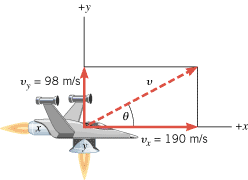 | | Figure 3.7
The magnitude of the velocity vector gives the speed of the spacecraft, and the angle q gives the direction of travel relative to the positive x direction. |
|
The direction of the velocity vector is given by the angle q in the drawing:
After 7.0 s, the spacecraft has a velocity of 210 m/s in a direction of 27° above the positive x axis. The craft is 740 m to the right and 390 m above the origin, as in Figure 3.5.
|
|
 |
| Check Your Understanding 2 |
 |
|
A power boat, starting from rest, maintains a constant acceleration. After a certain time t, its displacement and velocity are r and v. At a time 2t, what would be its displacement and velocity, assuming the acceleration remains the same?
(a) 2r and 2v (b) 2r and 4v (c) 4r and 2v (d) 4r and 4v
Background:
When an object accelerates, its displacement and velocity depend on time. If the acceleration is constant, the equations of kinematics in Table 3.1 apply.
For similar questions (including calculational counterparts), consult Self-Assessment Test 3.1. This test is described at the end of Section 3.3.
|
|
 |
The following Reasoning Strategy gives an overview of how the equations of kinematics are applied to describe motion in two dimensions, such as that in Example 1.
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |


![]() =
=![]() 0 s, so that r0
0 s, so that r0![]() =
=![]() 0 m. At a later time t, the spacecraft’s displacement is Dr
0 m. At a later time t, the spacecraft’s displacement is Dr![]() =
=![]() r–r0
r–r0![]() =
=![]() r. Relative to the x and y axes, the displacement r has vector components of x and y, respectively.
r. Relative to the x and y axes, the displacement r has vector components of x and y, respectively.

![]() CONCEPTS AT A GLANCE The independence of the x and y motions lies at the heart of two-dimensional kinematics. It allows us to treat two-dimensional motion as two distinct one-dimensional motions, one for the x direction and one for the y direction. As the Concepts-at-a-Glance chart in Figure 3.6 illustrates, everything that we have learned in Chapter 2 about kinematics in one dimension will now be applied separately to each of the two directions. In so doing, we will be able to describe the x and y variables separately and then bring these descriptions together to understand the two-dimensional picture. Example 4 takes this approach in dealing with a moving spacecraft.
CONCEPTS AT A GLANCE The independence of the x and y motions lies at the heart of two-dimensional kinematics. It allows us to treat two-dimensional motion as two distinct one-dimensional motions, one for the x direction and one for the y direction. As the Concepts-at-a-Glance chart in Figure 3.6 illustrates, everything that we have learned in Chapter 2 about kinematics in one dimension will now be applied separately to each of the two directions. In so doing, we will be able to describe the x and y variables separately and then bring these descriptions together to understand the two-dimensional picture. Example 4 takes this approach in dealing with a moving spacecraft.