16.3.
The Speed of a Wave on a String
The properties of the material
or medium through which a wave travels determine the speed of the wave. For example, Figure 16.8 shows a transverse wave on a string and draws attention to four string particles that have been drawn as colored dots. As the wave moves to the right, each particle is displaced, one after the other, from its undisturbed position. In the drawing, particles 1 and 2 have already been displaced upward, while particles 3 and 4 are not yet affected by the wave. Particle 3 will be next to move because the section of string immediately to its left (i.e., particle 2) will pull it upward.
 | | Figure 16.8
As a transverse wave moves to the right with speed v, each string particle is displaced, one after the other, from its undisturbed position. |
|
Figure 16.8 leads us to conclude that the speed with which the wave moves to the right depends on how quickly one particle of the string is accelerated upward in response to the net pulling force exerted by its adjacent neighbors. In accord with Newton’s second law, a stronger net force results in a greater acceleration, and, thus, a faster-moving wave. The ability of one particle to pull on its neighbors depends on how tightly the string is stretched—that is, on the tension (see Section 4.10 for a review of tension). The greater the tension, the greater the pulling force the particles exert on each other, and the faster the wave travels, other things being equal. Along with the tension, a second factor influences the wave speed. According to Newton’s second law, the inertia or mass of particle 3 in Figure 16.8 also affects how quickly it responds to the upward pull of particle 2. For a given net pulling force, a smaller mass has a greater acceleration than a larger mass. Therefore, other things being equal, a wave travels faster on a string whose particles have a small mass, or, as it turns out, on a string that has a small mass per unit length. The mass per unit length is called the linear density of the string. It is the mass m of the string divided by its length L, or m/L. The effects of the tension F and the mass per unit length are evident in the following expression for the speed v of a small-amplitude wave on a string:
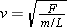 | (16.2) |  |
The motion of transverse waves along a string is important in the operation of musical instruments, such as the guitar, the violin, and the piano. In these instruments, the strings are either plucked, bowed, or struck to produce transverse waves. Example 2 discusses the speed of the waves on the strings of a guitar.
 Concept Simulation 16.1 Concept Simulation 16.1 |
 |
This simulation displays a wave traveling on a string and allows you to adjust the amplitude and frequency of the wave, as well as the thickness or mass of the string. The effect of your adjustments on the wavelength of the wave is displayed, as is the time for the wave to travel the length of the string. From the travel time you can assess how the speed of the wave depends on the mass of the string. |
|
 |
| Example 2 Waves Traveling on Guitar Strings |
 |
|
Transverse waves travel on the strings of an electric guitar after the strings are plucked (see Figure 16.9). The length of each string between its two fixed ends is 0.628 m, and the mass is 0.208 g for the highest pitched E string and 3.32 g for the lowest pitched E string. Each string is under a tension of 226 N. Find the speeds of the waves on the two strings.
 | | Figure 16.9
Plucking a guitar string generates transverse waves. |
|
Reasoning
The speed of a wave on a guitar string, as expressed by Equation 16.2, depends on the tension F in the string and its linear density m/L. Since the tension is the same for both strings, and smaller linear densities give rise to greater speeds, we expect the wave speed to be greatest on the string with the smallest linear density.
Solution
The speeds of the waves are given by Equation 16.2 as
Notice how fast the waves move; the speeds correspond to 1850 and 463 mi/h.
|
 |
Conceptual Example 3 offers additional insight into the nature of a wave as a traveling disturbance.
| Conceptual Example 3 Wave Speed Versus Particle Speed |
 |
|
Is the speed of a transverse wave on a string the same as the speed at which a particle on the string moves (see Figure 16.10)?
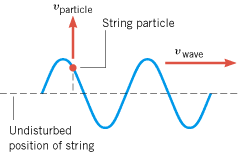 | | Figure 16.10
A transverse wave on a string is moving to the right with a constant speed vwave. A string particle moves up and down in simple harmonic motion about the undisturbed position of the string. The speed of the particle vparticle changes from moment to moment as the wave passes. |
|
Reasoning and Solution The particle speed vparticle specifies how fast the particle is moving as it oscillates up and down, and it is different from the wave speed. If the source of the wave (e.g., the hand in Figure 16.2c) vibrates in simple harmonic motion, each string particle vibrates in a like manner, with the same amplitude and frequency as the source. Moreover, the particle speed, unlike the wave speed, is not constant. As for any object in simple harmonic motion, the particle speed is greatest when the particle is passing through the undisturbed position of the string and zero when the particle is at its maximum displacement. According to Equation 10.7, the particle speed depends on the amplitude A, the angular frequency w, and the time t through the relation vparticle = = Aw sin wt, where the minus sign has been omitted because we are interested only in the speed, which is the magnitude of the particle’s velocity. Thus, the speed of a string particle is determined by the properties of the source creating the wave and not by the properties of the string itself. In contrast, the speed of the wave is determined by the properties of the string—that is, the tension F and the mass per unit length m/L, according to Equation 16.2. We see, then, that the two speeds, vwave and vparticle, are not the same. Aw sin wt, where the minus sign has been omitted because we are interested only in the speed, which is the magnitude of the particle’s velocity. Thus, the speed of a string particle is determined by the properties of the source creating the wave and not by the properties of the string itself. In contrast, the speed of the wave is determined by the properties of the string—that is, the tension F and the mass per unit length m/L, according to Equation 16.2. We see, then, that the two speeds, vwave and vparticle, are not the same.
Related Homework:
Conceptual Question 4, Problems 18, 99
|
 |
| Check Your Understanding 1 |
 |
|
String I and string II have the same length. However, the mass of string I is twice the mass of string II, and the tension in string I is eight times the tension in string II. A wave of the same amplitude and frequency travels on each of these strings. Which of the pictures in the drawing correctly shows the waves?
Background:
This question deals with the relationship between the frequency, wavelength, and speed of a traveling wave. It also deals with the factors that determine the speed of a wave on a string.
For similar questions (including calculational counterparts), consult Self-Assessment Test 16.1. This test is described at the end of Section 16.4.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |


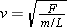
 Concept Simulation 16.1
Concept Simulation 16.1