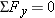|
Equilibrium Applications of Newton's Laws of Motion |
 |
 |
Concepts at a Glance The concept of equilibrium arises directly from Newton's second law. The Concepts-at-a-Glance chart in Figure 4.27 illustrates this important point. When the acceleration of an object is zero (
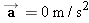
), the object is in equilibrium, as the upper-right part of the chart indicates. The present section includes several examples
involving equilibrium situations. On the other hand, when the acceleration is not zero (
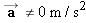
), we have a nonequilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton's second law.
 |
 |
 |
 |
 |
| Both, Mike Powell/Allsport/Getty Images |
 |
|
|
 |
| Figure 4.27 |
Concepts at a Glance Both equilibrium and nonequilibrium problems can be solved with the aid of Newton's second law. For equilibrium situations,
such as the gymnast holding the “Iron Cross” position in the left photograph, the acceleration is zero (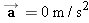 ). For nonequilibrium situations, such as the freely falling gymnast in the right photograph, the acceleration is not zero
( ). For nonequilibrium situations, such as the freely falling gymnast in the right photograph, the acceleration is not zero
(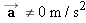 ). ).
|
|
 |
|
 |
Since the acceleration is zero for an object in equilibrium, all of the acceleration components are also zero. In two dimensions,
this means that
ax = 0 m/s
2 and
ay = 0 m/s
2. Substituting these values into the second law (Σ
Fx =
max and Σ
Fy =
may) shows that the
x component and the
y component of the net force must each be zero. In other words, the forces acting on an object in equilibrium must balance.
Thus, in two dimensions, the equilibrium condition is expressed by two equations:
In using Equations 4.9a and 4.9b to solve equilibrium problems, we will use the following five-step reasoning strategy:
Example 11 illustrates how these steps are followed. It deals with a traction device in which three forces act together to bring about
the equilibrium.
 |
 |
 |
Example 11 Traction for the Foot |
|
 |
 |
 |
 |
|
 |
 |
|
The physics of traction for a foot injury.
|
|
|
Figure 4.28 a shows a traction device used with a foot injury. The weight of the 2.2-kg object creates a tension in the rope that passes
around the pulleys. Therefore, tension forces 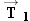 and 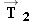 are applied to the pulley on the foot. (It may seem surprising that the rope applies a force to either side of the foot pulley.
A similar effect occurs when you place a finger inside a rubber band and push downward. You can feel each side of the rubber
band pulling upward on the finger.) The foot pulley is kept in equilibrium because the foot also applies a force  to it. This force arises in reaction (Newton's third law) to the pulling effect of the forces 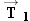 and 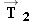 . Ignoring the weight of the foot, find the magnitude of  .
 |
 |
|
|
 |
| Figure 4.28 |
 |
|
(a)
|
A traction device for the foot.
|
 |
|
(b)
|
The free-body diagram for the pulley on the foot.
|
|
|
|
 |
|
 |
Reasoning
The forces 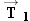 , , 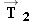 , and , and  keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum
of the x components and the sum of the y components of the three forces must each be zero. Figure 4.28b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum
of the x components and the sum of the y components of the three forces must each be zero. Figure 4.28b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force  , and the components of the forces , and the components of the forces 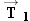 and and 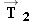 are indicated in the drawing. (See Section 1.7 for a review of vector components.) are indicated in the drawing. (See Section 1.7 for a review of vector components.)
Solution
 |
|
|
 |
Choose the orientation of the x, y axes for convenience. In Example 11, the axes have been rotated so the force  points along the x axis. Since  does not have a component along the y axis, the analysis is simplified.
|
|
|
Since the sum of the y components of the forces is zero, it follows that
or T1 = T2. In other words, the magnitudes of the tension forces are equal. In addition, the sum of the x components of the forces is zero, so we have that
Solving for F and letting T1 = T2 = T, we find that F = 2 T cos 35°. However, the tension T in the rope is determined by the weight of the 2.2-kg object: T = mg, where m is its mass and g is the acceleration due to gravity. Therefore, the magnitude of  is
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
Example 12 presents another situation in which three forces are responsible for the equilibrium of an object. However, in this example
all the forces have different magnitudes.
 |
 |
 |
Example 12 Replacing an Engine |
|
 |
 |
 |
 |
|
An automobile engine has a weight 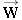 , whose magnitude is W = 3150 N. This engine is being positioned above an engine compartment, as Figure 4.29 a illustrates. To position the engine, a worker is using a rope. Find the tension 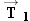 in the supporting cable and the tension 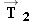 in the positioning rope.
 |
 |
|
|
 |
| Figure 4.29 |
 |
|
(a)
|
The ring is in equilibrium because of the three forces  (the tension force in the supporting cable), 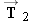 (the tension force in the positioning rope), and 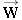 (the weight of the engine).
|
 |
|
(b)
|
The free-body diagram for the ring.
|
|
|
|
 |
|
 |
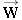 , , 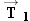 , and , and 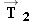 the ring in Figure 4.29a is at rest and, therefore, in equilibrium. Consequently, the sum of the x components and the sum of the y components of these forces must each be zero; ΣFx = 0 and ΣFy = 0. By using these relations, we can find T1 and T2. Figure 4.29b shows the free-body diagram of the ring and the force components for a suitable x, y axis system. the ring in Figure 4.29a is at rest and, therefore, in equilibrium. Consequently, the sum of the x components and the sum of the y components of these forces must each be zero; ΣFx = 0 and ΣFy = 0. By using these relations, we can find T1 and T2. Figure 4.29b shows the free-body diagram of the ring and the force components for a suitable x, y axis system.
Solution
 |
|
|
 |
When an object is in equilibrium, as here in Example 12, the net force is zero, 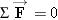 . This does not mean that each individual force is zero. It means that the vector sum of all the forces is zero.
|
|
|
The free-body diagram shows the components for each of the three forces, and the components are listed in the following table:
 |
 |
|
Force
|
x Component
|
y Component
|
|
|
-T1 sin 10.0°
|
+T1 cos 10.0°
|
|
|
+T2 sin 80.0°
|
-T2 cos 80.0°
|
|
|
0
|
-W
|
|
|
|
|
 |
|
 |
The plus signs in the table denote components that point along the positive axes, and the minus signs denote components that
point along the negative axes. Setting the sum of the x components and the sum of the y components equal to zero leads to the following equations:
Solving the first of these equations for T1 shows that
Substituting this expression for T1 into the second equation gives
Setting W = 3150 N in this result yields 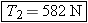 .
Since 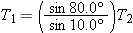 and T2 = 582 N, it follows that 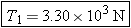 .
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
An object can be moving and still be in equilibrium, provided there is no acceleration. Example 13 illustrates such a case, and the solution is again obtained using the five-step reasoning strategy summarized at the beginning
of the section.
 |
 |
 |
Example 13 Equilibrium at Constant Velocity |
|
 |
 |
 |
 |
|
A jet plane is flying with a constant speed along a straight line, at an angle of 30.0° above the horizontal, as Figure 4.30 a indicates. The plane has a weight 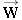 whose magnitude is W = 86 500 N, and its engines provide a forward thrust 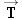 of magnitude T = 103 000 N. In addition, the lift force 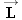 (directed perpendicular to the wings) and the force 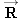 of air resistance (directed opposite to the motion) act on the plane. Find 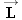 and 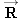 .
 |
 |
|
|
 |
| Figure 4.30 |
 |
|
(a)
|
A plane moves with a constant velocity at an angle of 30.0° above the horizontal due to the action of four forces, the weight
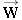 , the lift 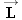 , the engine thrust 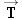 , and the air resistance 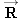 .
|
 |
|
(b)
|
The free-body diagram for the plane.
|
 |
|
(c)
|
This geometry occurs often in physics.
|
|
|
|
 |
|
 |
 |
|
|
 |
|
A moving object is in equilibrium if it moves with a constant velocity; then its acceleration is zero. A zero acceleration
is the fundamental characteristic of an object in equilibrium.
|
|
|
Reasoning
Figure 4.30b shows the free-body diagram of the plane, including the forces 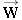 , , 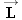 , , 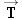 , and , and 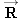 . Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force . Since the plane is not accelerating, it is in equilibrium, and the sum of the x components and the sum of the y components of these forces must be zero. The lift force 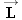 and the force and the force 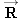 of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in
the free-body diagram that are rotated by 30.0° from their usual horizontal–vertical positions. This has been done purely
for convenience, since the weight of air resistance can be obtained from these equilibrium conditions. To calculate the components, we have chosen axes in
the free-body diagram that are rotated by 30.0° from their usual horizontal–vertical positions. This has been done purely
for convenience, since the weight 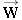 is then the only force that does not lie along either axis. is then the only force that does not lie along either axis.
Solution
When determining the components of the weight, it is necessary to realize that the angle β in Figure 4.30 a is 30.0°. Part c of the drawing focuses attention on the geometry that is responsible for this fact. There it can be seen that α + β = 90°
and α + 30.0° = 90°, with the result that β = 30.0°. The table below lists the components of the forces that act on the jet.
 |
 |
|
Force
|
x Component
|
y Component
|
|
|
-W sin 30.0°
|
-W cos 30.0°
|
|
|
0
|
+L
|
|
|
+T
|
0
|
|
|
-R
|
0
|
|
|
|
|
 |
|
 |
Setting the sum of the x component of the forces to zero gives
Setting the sum of the y component of the forces to zero gives
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
Check Your Understanding |
|
 |
 |
 |
 |
|
(The answer is given at the end of the book.)
|
 |
| 19. |
In which one of the following situations could an object possibly be in equilibrium?
|
(a)
|
Three forces act on the object; the forces all point along the same line but may have different directions.
|
 |
|
(b)
|
Two perpendicular forces act on the object.
|
 |
|
(c)
|
A single force acts on the object.
|
 |
|
(d)
|
In none of the situations described in (a), (b), and (c) could the object possibly be in equilibrium.
|
 |
|
 |
 |
| 20. |
A stone is thrown from the top of a cliff. Air resistance is negligible. As the stone falls, is it
|
(a)
|
in equilibrium or
|
 |
|
(b)
|
not in equilibrium?
|
 |
|
 |
 |
| 21. |
During the final stages of descent, a sky diver with an open parachute approaches the ground with a constant velocity. There
is no wind to blow him from side to side. Which one of the following statements is true?
|
(a)
|
The sky diver is not in equilibrium.
|
 |
|
(b)
|
The force of gravity is the only force acting on the sky diver, so that he is in equilibrium.
|
 |
|
(c)
|
The sky diver is in equilibrium because no forces are acting on him.
|
 |
|
(d)
|
The sky diver is in equilibrium because two forces act on him, the downward-acting force of gravity and the upward-acting
force of the parachute.
|
 |
|
 |
 |
| 22. |
A crate hangs from a ring at the middle of a rope, as the drawing illustrates. A person is pulling on the right end of the
rope to keep the crate in equilibrium. Can the rope ever be made to be perfectly horizontal?
|
 |
 |
|
|
 |
 |
|
 |
 |
 |
 |
 |
 |
| Copyright © 2010 John Wiley & Sons, Inc. All rights reserved. |


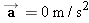 ), the object is in equilibrium, as the upper-right part of the chart indicates. The present section includes several examples
involving equilibrium situations. On the other hand, when the acceleration is not zero (
), the object is in equilibrium, as the upper-right part of the chart indicates. The present section includes several examples
involving equilibrium situations. On the other hand, when the acceleration is not zero (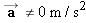 ), we have a nonequilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton's second law.
), we have a nonequilibrium situation, as the lower-right part of the chart suggests. Section 4.12 deals with nonequilibrium applications of Newton's second law.