 | Problems |
|
|
In several of the problems that follow, you are asked to graph position, velocity, and acceleration versus time. Usually a sketch will suffice, appropriately labeled and with straight and curved portions apparent. If you have a computer or graphing calculator, you might use it to produce the graph.
sec. 2-4 Average Velocity and Average Speed
| •1
During a hard sneeze, your eyes might shut for 0.50 s. If you are driving a car at 90 km/h during such a sneeze, how far does the car move during that time?
|  | |
| •2
The 1992 world speed record for a bicycle (human powered vehicle) was set by Chris Huber. His time through the measured 200 m stretch was a sizzling 6.509 s, at which he commented, “Cogito ergo zoom!” (I think, therefore I go fast!). In 2001, Sam Whittingham beat Huber's record by 19.0 km/h. What was Whittingham's time through the 200 m?
|  | |
| •3
An automobile travels on a straight road for 40 km at 30 km/h. It then continues in the same direction for another 40 km at 60 km/h. (a) What is the average velocity of the car during this 80 km trip? (Assume that it moves in the positive x direction.) (b) What is the average speed? (c) Graph x versus t and indicate how the average velocity is found on the graph.
|  | |
| •4
A car travels up a hill at a constant speed of 40 km/h and returns down the hill at a constant speed of 60 km/h. Calculate the average speed for the round trip.
|  | |
| •5
The position of an object moving along an x axis is given by x = 3t - 4t2 + t3, where x is in meters and t in seconds. Find the position of the object at the following values of t: (a) 1 s, (b) 2 s, (c) 3 s, and (d) 4 s. (e) What is the object's displacement between t = 0 and t = 4 s? (f) What is its average velocity for the time interval from t = 2 s to t = 4 s? (g) Graph x versus t for 0 ≤ t ≤ 4 s and indicate how the answer for (f) can be found on the graph.
|  | |
| •6
Compute your average velocity in the following two cases: (a) You walk 73.2 m at a speed of 1.22 m/s and then run 73.2 m at a speed of 3.05 m/s along a straight track. (b) You walk for 1.00 min at a speed of 1.22 m/s and then run for 1.00 min at 3.05 m/s along a straight track. (c) Graph x versus t for both cases and indicate how the average velocity is found on the graph.
|  | |
| •7
The position function x(t) of a particle moving along an x axis is x = 4.0 - 6.0t2, with x in meters and t in seconds. (a) At what time and (b) where does the particle (momentarily) stop? At what (c) negative time and (d) positive time does the particle pass through the origin? (e) Graph x versus t for the range -5 s to +5 s. (f) To shift the curve rightward on the graph, should we include the term +20t or the term -20t in x(t)? (g) Does that inclusion increase or decrease the value of x at which the particle momentarily stops?
|  | |
| ••8
You are to drive to an interview in another town, at a distance of 300 km on an expressway. The interview is at 11:15 A.M. You plan to drive at 100 km/h, so you leave at 8:00 A.M. to allow some extra time. You drive at that speed for the first 100 km, but then construction work forces you to slow to 40 km/h for 40 km. What would be the least speed needed for the rest of the trip to arrive in time for the interview?
|  | |
| ••9
In 1 km races, runner 1 on track 1 (with time 2 min, 27.95 s) appears to be faster than runner 2 on track 2 (2 min, 28.15 s). However, length L2 of track 2 might be slightly greater than length L1 of track 1. How large can L2 - L1 be for us still to conclude that runner 1 is faster?
|  | |
| ••10
Two trains, each having a speed of 30 km/h, are headed at each other on the same straight track. A bird that can fly 60 km/h flies off the front of one train when they are 60 km apart and heads directly for the other train. On reaching the other train, the bird flies directly back to the first train, and so forth. (We have no idea why a bird would behave in this way.) What is the total distance the bird travels before the trains collide?
|  | |
| •••11
You drive on Interstate 10 from San Antonio to Houston, half the time at 55 km/h and the other half at 90 km/h. On the way back you travel half the distance at 55 km/h and the other half at 90 km/h. What is your average speed (a) from San Antonio to Houston, (b) from Houston back to San Antonio, and (c) for the entire trip? (d) What is your average velocity for the entire trip? (e) Sketch x versus t for (a), assuming the motion is all in the positive x direction. Indicate how the average velocity can be found on the sketch.
|  | |
sec. 2-5 Instantaneous Velocity and Speed
| •12
(a) If a particle's position is given by x = 4 - 12t + 3t2 (where t is in seconds and x is in meters), what is its velocity at t = 1 s? (b) Is it moving in the positive or negative direction of x just then? (c) What is its speed just then? (d) Is the speed increasing or decreasing just then? (Try answering the next two questions without further calculation.) (e) Is there ever an instant when the velocity is zero? If so, give the time t; if not, answer no. (f) Is there a time after t = 3 s when the particle is moving in the negative direction of x? If so, give the time t; if not, answer no.
|  | |
| ••13
The position of a particle moving along the x axis is given in centimeters by x = 9.75 + 1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t = 2.00 s to t = 3.00 s; (b) the instantaneous velocity at t = 2.00 s; (c) the instantaneous velocity at t = 3.00 s; (d) the instantaneous velocity at t = 2.50 s; and (e) the instantaneous velocity when the particle is midway between its positions at t = 2.00 s and t = 3.00 s. (f) Graph x versus t and indicate your answers graphically.
|  | |
sec. 2-6 Acceleration
| •14
(a) If the position of a particle is given by x = 20t - 5t3, where x is in meters and t is in seconds, when, if ever, is the particle's velocity zero? (b) When is its acceleration a zero? (c) For what time range (positive or negative) is a negative? (d) Positive? (e) Graph x(t), v(t), and a(t).
|  | |
| •15
At a certain time a particle had a speed of 18 m/s in the positive x direction, and 2.4 s later its speed was 30 m/s in the opposite direction. What is the average acceleration of the particle during this 2.4 s interval?
|  | |
| •16
An electron moving along the x axis has a position given by x = 16te-t m, where t is in seconds. How far is the electron from the origin when it momentarily stops?
|  | |
| •17
The position of a particle moving along an x axis is given by x = 12t2 - 2t3, where x is in meters and t is in seconds. Determine (a) the position, (b) the velocity, and (c) the acceleration of the particle at t = 3.0 s. (d) What is the maximum positive coordinate reached by the particle and (e) at what time is it reached? (f) What is the maximum positive velocity reached by the particle and (g) at what time is it reached? (h) What is the acceleration of the particle at the instant the particle is not moving (other than at t = 0)? (i) Determine the average velocity of the particle between t = 0 and t = 3 s.
|  | |
| •18
From t = 0 to t = 5.00 min, a man stands still, and from t = 5.00 min to t = 10.0 min, he walks briskly in a straight line at a constant speed of 2.20 m/s. What are (a) his average velocity vavg and (b) his average acceleration aavg in the time interval 2.00 min to 8.00 min? What are (c) vavg and (d) aavg in the time interval 3.00 min to 9.00 min? (e) Sketch x versus t and v versus t, and indicate how the answers to (a) through (d) can be obtained from the graphs.
|  | |
| ••19
The position of a particle moving along the x axis depends on the time according to the equation x = ct2 - bt3, where x is in meters and t in seconds. What are the units of (a) constant c and (b) constant b? Let their numerical values be 3.0 and 2.0, respectively. (c) At what time does the particle reach its maximum positive x position? From t = 0.0 s to t = 4.0 s, (d) what distance does the particle move and (e) what is its displacement? Find its velocity at times (f) 1.0 s, (g) 2.0 s, (h) 3.0 s, and (i) 4.0 s. Find its acceleration at times (j) 1.0 s, (k) 2.0 s, (l) 3.0 s, and (m) 4.0 s.
|  | |
sec. 2-7 Constant Acceleration: A Special Case
| •20
A muon (an elementary particle) enters a region with a speed of 5.00 × 106 m/s and then is slowed at the rate of 1.25 × 1014 m/s2. (a) How far does the muon take to stop? (b) Graph x versus t and v versus t for the muon.
|  | |
| •21
An electron has a constant acceleration of +3.2 m/s2. At a certain instant its velocity is +9.6 m/s. What is its velocity (a) 2.5 s earlier and (b) 2.5 s later?
|  | |
| •22
On a dry road, a car with good tires may be able to brake with a constant deceleration of 4.92 m/s2. (a) How long does such a car, initially traveling at 24.6 m/s, take to stop? (b) How far does it travel in this time? (c) Graph x versus t and v versus t for the deceleration.
|  | |
| •23
Suppose a rocket ship in deep space moves with constant acceleration equal to 9.8 m/s2, which gives the illusion of normal gravity during the flight. (a) If it starts from rest, how long will it take to acquire a speed one-tenth that of light, which travels at 3.0 × 108 m/s? (b) How far will it travel in so doing?
|  | |
| •24
An electric vehicle starts from rest and accelerates at a rate of 2.0 m/s2 in a straight line until it reaches a speed of 20 m/s. The vehicle then slows at a constant rate of 1.0 m/s2 until it stops. (a) How much time elapses from start to stop? (b) How far does the vehicle travel from start to stop?
|  | |
•25
An electron with initial velocity v0 = 1.50 × 105 m/s enters a region of length L = 1.00 cm where it is electrically accelerated (Figure 2-19). It emerges with v = 5.70 × 106 m/s. What is its acceleration, assumed constant? (Such a process occurs in old-fashion television sets.)
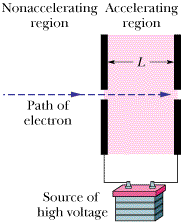 | | Fig. 2-19 Problem 25.
|
|  | |
| •26
A world's land speed record was set by Colonel John P. Stapp when in March 1954 he rode a rocket-propelled sled that moved along a track at 1020 km/h. He and the sled were brought to a stop in 1.4 s. (See Figure 2-7.) In terms of g, what acceleration did he experience while stopping?
|  | |
| •27
A car traveling 56.0 km/h is 24.0 m from a barrier when the driver slams on the brakes. The car hits the barrier 2.00 s later. (a) What is the magnitude of the car's constant acceleration before impact? (b) How fast is the car traveling at impact?
|  | |
| •28
The brakes on your car can slow you at a rate of 5.2 m/s2. (a) If you are going 137 km/h and suddenly see a state trooper, what is the minimum time in which you can get your car under the 90 km/h speed limit? (The answer reveals the futility of braking to keep your high speed from being detected with a radar or laser gun.) (b) Graph x versus t and v versus t for such a slowing.
|  | |
| •29
A certain elevator cab has a total run of 190 m and a maximum speed of 305 m/min, and it accelerates from rest and then back to rest at 1.22 m/s2. (a) How far does the cab move while accelerating to full speed from rest? (b) How long does it take to make the nonstop 190 m run, starting and ending at rest?
|  | |
| ••30
A car moves along an x axis through a distance of 900 m, starting at rest (at x = 0) and ending at rest (at x = 900 m). Through the first ¼ of that distance, its acceleration is +2.25 m/s2. Through the next ¾ of that distance, its acceleration is -0.750 m/s2. What are (a) its travel time through the 900 m and (b) its maximum speed? (c) Graph position x, velocity v, and acceleration a versus time t for the trip.
|  | |
••31
Figure 2-20 depicts the motion of a particle moving along an x axis with a constant acceleration. What are the (a) magnitude and (b) direction of the particle's acceleration?
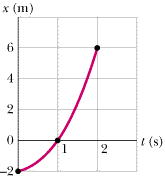 | | Fig. 2-20 Problem 31.
|
|  | |
| ••32
You are arguing over a cell phone while trailing an unmarked police car by 25 m; both your car and the police car are traveling at 110 km/h. Your argument diverts your attention from the police car for 2.0 s (long enough for you to look at the phone and yell, “I won't do that!”). At the beginning of that 2.0 s, the police officer begins braking suddenly at 5.0 m/s2. (a) What is the separation between the two cars when your attention finally returns? Suppose that you take another 0.40 s to realize your danger and begin braking. (b) If you too brake at 5.0 m/s2, what is your speed when you hit the police car?
|  | |
••33
Cars A and B move in the same direction in adjacent lanes. The position x of car A is given in Figure 2-21, from time t = 0 to t = 7.0 s. At t = 0, car B is at x = 0, with a velocity of 12 m/s and a negative constant acceleration aB. (a) What must aB be such that the cars are (momentarily) side by side (momentarily at the same value of x) at t = 4.0 s? (b) For that value of aB, how many times are the cars side by side? (c) Sketch the position x of car B versus time t on Figure 2-21. How many times will the cars be side by side if the magnitude of acceleration aB is (d) more than and (e) less than the answer to part (a)?
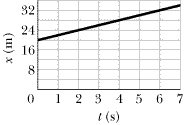 | | Fig. 2-21 Problem 33.
|
|  | |
| ••34
(a) If the maximum acceleration that is tolerable for passengers in a subway train is 1.34 m/s2 and subway stations are located 806 m apart, what is the maximum speed a subway train can attain between stations? (b) What is the travel time between stations? (c) If a subway train stops for 20 s at each station, what is the maximum average speed of the train, from one start-up to the next? (d) Graph x, v, and a versus t for the interval from one start-up to the next.
|  | |
••35
As two trains move along a track, their conductors suddenly notice that they are headed toward each other. Figure 2-22 gives their velocities v as functions of time t as the conductors slow the trains. The slowing processes begin when the trains are 200 m apart. What is their separation when both trains have stopped?
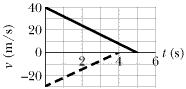 | | Fig. 2-22 Problem 35.
|
|  | |
••36
In Figure 2-23, a red car and a green car, identical except for the color, move toward each other in adjacent lanes and parallel to an x axis. At time t = 0, the red car is at xr = 0 and the green car is at xg = 220 m. If the red car has a constant velocity of 20 km/h, the cars pass each other at x = 44.5 m, and if it has a constant velocity of 40 km/h, they pass each other at x = 76.6 m. What are (a) the initial velocity and (b) the acceleration of the green car?
 | | Fig. 2-23 Problem 36.
|
|  | |
•••37
When a high-speed passenger train traveling at 161 km/h rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance D = 676 m ahead (Figure 2-24). The locomotive is moving at 29.0 km/h. The engineer of the high-speed train immediately applies the brakes. (a) What must be the magnitude of the resulting constant deceleration if a collision is to be just avoided? (b) Assume that the engineer is at x = 0 when, at t = 0, he first spots the locomotive. Sketch x(t) curves for the locomotive and high-speed train for the cases in which a collision is just avoided and is not quite avoided.
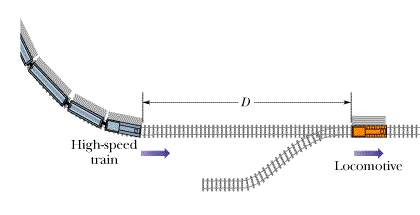 | | Fig. 2-24 Problem 37.
|
|  | |
sec. 2-9 Free-Fall Acceleration
| •38
A hoodlum throws a stone vertically downward with an initial speed of 12.0 m/s from the roof of a building, 30.0 m above the ground. (a) How long does it take the stone to reach the ground? (b) What is the speed of the stone at impact?
|  | |
| •39
At a construction site a pipe wrench struck the ground with a speed of 24 m/s. (a) From what height was it inadvertently dropped? (b) How long was it falling? (c) Sketch graphs of y, v, and a versus t for the wrench.
|  | |
| •40
Raindrops fall 1700 m from a cloud to the ground. (a) If they were not slowed by air resistance, how fast would the drops be moving when they struck the ground? (b) Would it be safe to walk outside during a rainstorm?
|  | |
| •41
(a) With what speed must a ball be thrown vertically from ground level to rise to a maximum height of 50 m? (b) How long will it be in the air? (c) Sketch graphs of y, v, and a versus t for the ball. On the first two graphs, indicate the time at which 50 m is reached.
|  | |
| •42
A startled armadillo leaps upward, rising 0.544 m in the first 0.200 s. (a) What is its initial speed as it leaves the ground? (b) What is its speed at the height of 0.544 m? (c) How much higher does it go?
|  | |
| •43
A hot-air balloon is ascending at the rate of 12 m/s and is 80 m above the ground when a package is dropped over the side. (a) How long does the package take to reach the ground? (b) With what speed does it hit the ground?
|  | |
| ••44
A bolt is dropped from a bridge under construction, falling 90 m to the valley below the bridge. (a) In how much time does it pass through the last 20% of its fall? What is its speed (b) when it begins that last 20% of its fall and (c) when it reaches the valley beneath the bridge?
|  | |
••45
At time t = 0, apple 1 is dropped from a bridge onto a roadway beneath the bridge; somewhat later, apple 2 is thrown down from the same height. Figure 2-25 gives the vertical positions y of the apples versus t during the falling, until both apples have hit the roadway. With approximately what speed is apple 2 thrown down?
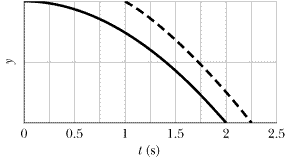 | | Fig. 2-25 Problem 45.
|
|  | |
••46
Figure 2-26 shows the speed v versus height y of a ball tossed directly upward, along a y axis. The speed at height yA is vA. The speed at height yB is ⅓vA. What is speed vA?
 | | Fig. 2-26 Problem 46.
|
|  | |
| ••47
A key falls from a bridge that is 45 m above the water. It falls directly into a model boat, moving with constant velocity, that is 12 m from the point of impact when the key is released. What is the speed of the boat?
|  | |
••48
As a runaway scientific balloon ascends at 19.6 m/s, one of its instrument packages breaks free of a harness and free-falls. Figure 2-27 gives the vertical velocity of the package versus time, from before it breaks free to when it reaches the ground. (a) What maximum height above the break-free point does it rise? (b) How high is the break-free point above the ground?
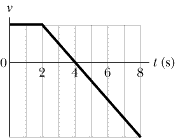 | | Fig. 2-27 Problem 48.
|
|  | |
| ••49
A ball of moist clay falls 15.0 m to the ground. It is in contact with the ground for 20.0 ms before stopping. (a) What is the magnitude of the average acceleration of the ball during the time it is in contact with the ground? (Treat the ball as a particle.) (b) Is the average acceleration up or down?
|  | |
| ••50
A rock is thrown vertically upward from ground level at time t = 0. At t = 1.5 s it passes the top of a tall tower, and 1.0 s later it reaches its maximum height. What is the height of the tower?
|  | |
| ••51
To test the quality of a tennis ball, you drop it onto the floor from a height of 4.00 m. It rebounds to a height of 2.00 m. If the ball is in contact with the floor for 12.0 ms, (a) what is the magnitude of its average acceleration during that contact and (b) is the average acceleration up or down?
|  | |
| ••52
A stone is dropped into a river from a bridge 43.9 m above the water. Another stone is thrown vertically down 1.00 s after the first is dropped. The stones strike the water at the same time. (a) What is the initial speed of the second stone? (b) Plot velocity versus time on a graph for each stone, taking zero time as the instant the first stone is released.
|  | |
| ••53
Water drips from the nozzle of a shower onto the floor 200 cm below. The drops fall at regular (equal) intervals of time, the first drop striking the floor at the instant the fourth drop begins to fall. When the first drop strikes the floor, how far below the nozzle are the (a) second and (b) third drops?
|  | |
| ••54
An object falls a distance h from rest. If it travels 0.50h in the last 1.00 s, find (a) the time and (b) the height of its fall. (c) Explain the physically unacceptable solution of the quadratic equation in t that you obtain.
|  | |
| ••55
A drowsy cat spots a flowerpot that sails first up and then down past an open window. The pot is in view for a total of 0.50 s, and the top-to-bottom height of the window is 2.00 m. How high above the window top does the flowerpot go?
|  | |
| •••56
A basketball player grabbing a rebound jumps 76.0 cm vertically. How much total time (ascent and descent) does the player spend (a) in the top 15.0 cm of this jump and (b) in the bottom 15.0 cm? Do your results explain why such players seem to hang in the air at the top of a jump?
|  | |
| •••57
A steel ball is dropped from a building's roof and passes a window, taking 0.125 s to fall from the top to the bottom of the window, a distance of 1.20 m. It then falls to a sidewalk and bounces back past the window, moving from bottom to top in 0.125 s. Assume that the upward flight is an exact reverse of the fall. The time the ball spends below the bottom of the window is 2.00 s. How tall is the building?
|  | |
•••58
A ball is shot vertically upward from the surface of a planet in a distant solar system. A plot of y versus t for the ball is shown in Figure 2-28, where y is the height of the ball above its starting point and t = 0 at the instant the ball is shot. What are the magnitudes of (a) the free-fall acceleration on the planet and (b) the initial velocity of the ball?
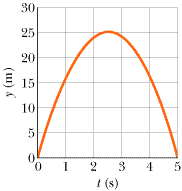 | | Fig. 2-28 Problem 58.
|
|  | |
sec. 2-10 Graphical Integration in Motion Analysis
| •59
In Sample Problem 2-8, at maximum head acceleration, what is the speed of (a) the head and (b) the torso?
|  | |
••60
In a forward punch in karate, the fist begins at rest at the waist and is brought rapidly forward until the arm is fully extended. The speed v(t) of the fist is given in Figure 2-29 for someone skilled in karate. How far has the fist moved at (a) time t = 50 ms and (b) when the speed of the fist is maximum?
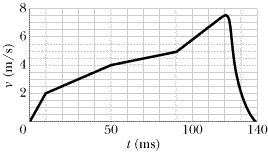 | | Fig. 2-29 Problem 60.
|
|  | |
••61
How far does the runner whose velocity-time graph is shown in Figure 2-30 travel in 16 s?
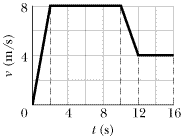 | | Fig. 2-30 Problem 61.
|
|  | |
••62
When a soccer ball is kicked toward a player and the player deflects the ball by “heading” it, the acceleration of the head during the collision can be significant. Figure 2-31 gives the measured acceleration a(t) of a soccer player's head for a bare head and a helmeted head, starting from rest. At time t = 7.0 ms, what is the difference in the speed acquired by the bare head and the speed acquired by the helmeted head?
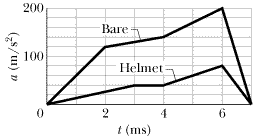 | | Fig. 2-31 Problem 62.
|
|  | |
Additional Problems
| 63
At the instant the traffic light turns green, an automobile starts with a constant acceleration a of 2.2 m/s2. At the same instant a truck, traveling with a constant speed of 9.5 m/s, overtakes and passes the automobile. (a) How far beyond the traffic signal will the automobile overtake the truck? (b) How fast will the automobile be traveling at that instant?
|  | |
| 64
A red train traveling at 72 km/h and a green train traveling at 144 km/h are headed toward each other along a straight, level track. When they are 950 m apart, each engineer sees the other's train and applies the brakes. The brakes slow each train at the rate of 1.0 m/s2. Is there a collision? If so, answer yes and give the speed of the red train and the speed of the green train at impact, respectively. If not, answer no and give the separation between the trains when they stop.
|  | |
65
At time t = 0, a rock climber accidentally allows a piton to fall freely from a high point on the rock wall to the valley below him. Then, after a short delay, his climbing partner, who is 10 m higher on the wall, throws a piton downward. The positions y of the pitons versus t during the falling are given in Figure 2-32. With what speed is the second piton thrown?
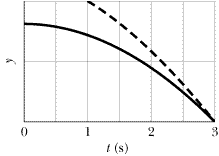 | | Fig. 2-32 Problem 65.
|
|  | |
| 66
In an arcade video game, a spot is programmed to move across the screen according to x = 9.00t - 0.750t3, where x is distance in centimeters measured from the left edge of the screen and t is time in seconds. When the spot reaches a screen edge, at either x = 0 or x = 15.0 cm, t is reset to 0 and the spot starts moving again according to x(t). (a) At what time after starting is the spot instantaneously at rest? (b) At what value of x does this occur? (c) What is the spot's acceleration (including sign) when this occurs? (d) Is it moving right or left just prior to coming to rest? (e) Just after? (f) At what time t > 0 does it first reach an edge of the screen?
|  | |
| 67
A rock is shot vertically upward from the edge of the top of a tall building. The rock reaches its maximum height above the top of the building 1.60 s after being shot. Then, after barely missing the edge of the building as it falls downward, the rock strikes the ground 6.00 s after it is launched. In SI units: (a) with what upward velocity is the rock shot, (b) what maximum height above the top of the building is reached by the rock, and (c) how tall is the building?
|  | |
| 68
A car moving with constant acceleration covered the distance between two points 60.0 m apart in 6.00 s. Its speed as it passed the second point was 15.0 m/s. (a) What was the speed at the first point? (b) What was the magnitude of the acceleration? (c) At what prior distance from the first point was the car at rest? (d) Graph x versus t and v versus t for the car, from rest (t = 0).
|  | |
69
An iceboat has a constant velocity toward the east when a sudden gust of wind causes the iceboat to have a constant acceleration toward the east for a period of 3.0 s. A plot of x versus t is shown in Figure 2-33, where t = 0 is taken to be the instant the wind starts to blow and the positive x axis is toward the east. (a) What is the acceleration of the iceboat during the 3.0 s interval? (b) What is the velocity of the iceboat at the end of the 3.0 s interval? (c) If the acceleration remains constant for an additional 3.0 s, how far does the iceboat travel during this second 3.0 s interval?
 | | Fig. 2-33 Problem 69.
|
|  | |
| 70
A rock is dropped from a 100-m-high cliff. How long does it take to fall (a) the first 50 m and (b) the second 50 m?
|  | |
| 71
You are driving toward a traffic signal when it turns yellow. Your speed is the legal speed limit of v0 = 55 km/h; your best deceleration rate has the magnitude a = 5.18 m/s2. Your best reaction time to begin braking is T = 0.75 s. To avoid having the front of your car enter the intersection after the light turns red, should you brake to a stop or continue to move at 55 km/h if the distance to the intersection and the duration of the yellow light are (a) 40 m and 2.8 s, and (b) 32 m and 1.8 s? Give an answer of brake, continue, either (if either strategy works), or neither (if neither strategy works).
|  | |
| 72
Two subway stops are separated by 1100 m. If a subway train accelerates at +1.2 m/s2 from rest through the first half of the distance and decelerates at -1.2 m/s2 through the second half, what are (a) its travel time and (b) its maximum speed? (c) Graph x, v, and a versus t for the trip.
|  | |
| 73
A car can be braked to a stop from the autobahn-like speed of 200 km/h in 170 m. Assuming the acceleration is constant, find its magnitude in (a) SI units and (b) in terms of g. (c) How much time Tb is required for the braking? Your reaction time Tr is the time you require to perceive an emergency, move your foot to the brake, and begin the braking. If Tr = 400 ms, then (d) what is Tb in terms of Tr, and (e) is most of the full time required to stop spent in reacting or braking? Dark sunglasses delay the visual signals sent from the eyes to the visual cortex in the brain, increasing Tr. (f) In the extreme case in which Tr is increased by 100 ms, how much farther along the road does the car travel during your reaction time?
|  | |
| 74
The sport with the fastest moving ball is jai alai, where measured speeds have reached 303 km/h. If a professional jai alai player faces a ball at that speed and involuntarily blinks, he blacks out the scene for 100 ms. How far does the ball move during the blackout?
|  | |
| 75
The acceleration of a particle along an x axis is a = 5.0t, with t in seconds and a in meters per second squared. At t = 2.0 s, its velocity is +17 m/s. What is its velocity at t = 4.0 s?
|  | |
| 76
The wings on a stonefly do not flap, and thus the insect cannot fly. However, when the insect is on a water surface, it can sail across the surface by lifting its wings into a breeze. Suppose that you time stoneflies as they move at constant speed along a straight path of a certain length. On average, the trips each take 7.1 s with the wings set as sails and 25.0 s with the wings tucked in. (a) What is the ratio of the sailing speed vs to the nonsailing speed vns? (b) In terms of vs, what is the difference in the times the insects take to travel the first 2.0 m along the path with and without sailing?
|  | |
| 77
Most important in an investigation of an airplane crash by the U.S. National Transportation Safety Board is the data stored on the airplane's flight-data recorder, commonly called the “black box” in spite of its orange coloring and reflective tape. The recorder is engineered to withstand a crash with an average deceleration of magnitude 3400g during a time interval of 6.50 ms. In such a crash, if the recorder and airplane have zero speed at the end of that time interval, what is their speed at the beginning of the interval?
|  | |
78
A graph of x versus t for a particle in straight-line motion is shown in Figure 2-34. (a) What is the average velocity of the particle between t = 0.50 s and t = 4.5 s? (b) What is the instantaneous velocity of the particle at t = 4.5 s? (c) What is the average acceleration of the particle between t = 0.50 s and t = 4.5 s? (d) What is the instantaneous acceleration of the particle at t = 4.5 s?
 | | Fig. 2-34 Problem 78.
|
|  | |
| 79
If the position of an object is given by x = 2.0t3, where x is measured in meters and t in seconds, find (a) the average velocity and (b) the average acceleration between t = 1.0 s and t = 2.0 s. Then find (c) the instantaneous velocity v and (d) the instantaneous acceleration a at t = 1.0 s. Next find (e) v and (f) a at t = 2.0 s. (g) Compare the average and instantaneous quantities and in each case explain why the larger one is larger. (h) Graph x versus t and v versus t, and indicate on the graphs your answers to (a) through (f).
|  | |
| 80
A lead ball is dropped in a lake from a diving board 5.20 m above the water. It hits the water with a certain velocity and then sinks to the bottom with this same constant velocity. It reaches the bottom 4.80 s after it is dropped. (a) How deep is the lake? What are the (b) magnitude and (c) direction (up or down) of the average velocity of the ball for the entire fall? Suppose that all the water is drained from the lake. The ball is now thrown from the diving board so that it again reaches the bottom in 4.80 s. What are the (d) magnitude and (e) direction of the initial velocity of the ball?
|  | |
| 81
From January 26, 1977, to September 18, 1983, George Meegan of Great Britain walked from Ushuaia, at the southern tip of South America, to Prudhoe Bay in Alaska, covering 30600 km. In meters per second, what was his average speed during that time period?
|  | |
82
A graph of acceleration a versus t time for a particle as it moves along an x axis is shown in Figure 2-35. At t = 0 the coordinate of the particle is 4.0 m and the velocity v is 2.0 m/s. (a) What is the velocity of the particle at t = 2.0 s? (b) Write an expression for v(t) in meters per second that is valid for the interval 2.0 s ≤ t ≤ 4.0 s.
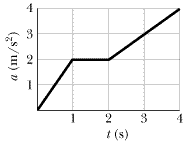 | | Fig. 2-35 Problem 82.
|
|  | |
| 83
A train started from rest and moved with constant acceleration. At one time it was traveling 30 m/s, and 160 m farther on it was traveling 50 m/s. Calculate (a) the acceleration, (b) the time required to travel the 160 m mentioned, (c) the time required to attain the speed of 30 m/s, and (d) the distance moved from rest to the time the train had a speed of 30 m/s. (e) Graph x versus t and v versus t for the train, from rest.
|  | |
| 84
The single cable supporting an unoccupied construction elevator breaks when the elevator is at rest at the top of a 120-m-high building. (a) With what speed does the elevator strike the ground? (b) How long is it falling? (c) What is its speed when it passes the halfway point on the way down? (d) How long has it been falling when it passes the halfway point?
|  | |
| 85
A rocket-driven sled running on a straight, level track is used to investigate the physiological effects of large accelerations on humans. One such sled can attain a speed of 1600 km/h in 1.8 s, starting from rest. Find (a) the acceleration (assumed constant) in terms of g and (b) the distance traveled.
|  | |
| 86
A certain sprinter has a top speed of 11.0 m/s. If the sprinter starts from rest and accelerates at a constant rate, he is able to reach his top speed in a distance of 12.0 m. He is then able to maintain this top speed for the remainder of a 100 m race. (a) What is his time for the 100 m race? (b) In order to improve his time, the sprinter tries to decrease the distance required for him to reach his top speed. What must this distance be if he is to achieve a time of 10.0 s for the race?
|  | |
| 87
A hot rod can accelerate from 0 to 60 km/h in 5.4 s. (a) What is its average acceleration, in m/s2, during this time? (b) How far will it travel during the 5.4 s, assuming its acceleration is constant? (c) From rest, how much time would it require to go a distance of 0.25 km if its acceleration could be maintained at the value in (a)?
|  | |
88
A particle starts from the origin at t = 0 and moves along the positive x axis. A graph of the velocity of the particle as a function of the time is shown in Figure 2-36. (a) What is the coordinate of the particle at t = 5.0 s? (b) What is the velocity of the particle at t = 5.0 s? (c) What is the acceleration of the particle at t = 5.0 s? (d) What is the average velocity of the particle between t = 1.0 s and t = 5.0 s? (e) What is the average acceleration of the particle between t = 1.0 s and t = 5.0 s?
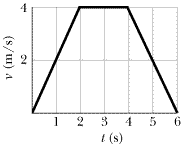 | | Fig. 2-36 Problem 88.
|
|  | |
| 89
A stone is thrown vertically upward. On its way up it passes point A with speed v, and point B, 3.00 m higher than A, with speed ½v. Calculate (a) the speed v and (b) the maximum height reached by the stone above point B.
|  | |
90
Figure 2-37 shows a simple device for measuring your reaction time. It consists of a cardboard strip marked with a scale and two large dots. A friend holds the strip vertically, with thumb and forefinger at the dot on the right in Figure 2-37. You then position your thumb and forefinger at the other dot (on the left in Figure 2-37), being careful not to touch the strip. Your friend releases the strip, and you try to pinch it as soon as possible after you see it begin to fall. The mark at the place where you pinch the strip gives your reaction time. (a) How far from the lower dot should you place the 50.0 ms mark? How much higher should you place the marks for (b) 100, (c) 150, (d) 200, and (e) 250 ms? (For example, should the 100 ms marker be 2 times as far from the dot as the 50 ms marker? If so, give an answer of 2 times. Can you find any pattern in the answers?)
 | | Fig. 2-37 Problem 90.
|
|  | |
| 91
A rock is dropped (from rest) from the top of a 60-m-tall building. How far above the ground is the rock 1.2 s before it reaches the ground?
|  | |
| 92
A ball is thrown vertically downward from the top of a 36.6-m-tall building. The ball passes the top of a window that is 12.2 m above the ground 2.00 s after being thrown. What is the speed of the ball as it passes the top of the window?
|  | |
| 93
A certain juggler usually tosses balls vertically to a height H. To what height must they be tossed if they are to spend twice as much time in the air?
|  | |
| 94
Two diamonds begin a free fall from rest from the same height, 1.0 s apart. How long after the first diamond begins to fall will the two diamonds be 10 m apart?
|  | |
| 95
To stop a car, first you require a certain reaction time to begin braking; then the car slows at a constant rate. Suppose that the total distance moved by your car during these two phases is 56.7 m when its initial speed is 80.5 km/h, and 24.4 m when its initial speed is 48.3 km/h. What are (a) your reaction time and (b) the magnitude of the acceleration?
|  | |
| 96
If a baseball pitcher throws a fastball at a horizontal speed of 160 km/h, how long does the ball take to reach home plate 18.4 m away?
|  | |
| 97
A proton moves along the x axis according to the equation x = 50t + 10t2, where x is in meters and t is in seconds. Calculate (a) the average velocity of the proton during the first 3.0 s of its motion, (b) the instantaneous velocity of the proton at t = 3.0 s, and (c) the instantaneous acceleration of the proton at t = 3.0 s. (d) Graph x versus t and indicate how the answer to (a) can be obtained from the plot. (e) Indicate the answer to (b) on the graph. (f) Plot v versus t and indicate on it the answer to (c).
|  | |
| 98
The speed of a bullet is measured to be 640 m/s as the bullet emerges from a barrel of length 1.20 m. Assuming constant acceleration, find the time that the bullet spends in the barrel after it is fired.
|  | |
99
Figure 2-38 gives the acceleration a versus time t for a particle moving along an x axis. At t = -2.0 s, the particle's velocity is 7.0 m/s. What is its velocity at t = 6.0 s?
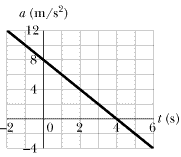 | | Fig. 2-38 Problem 99.
|
|  | |
| 100
A mining cart is pulled up a hill at 20 km/h and then pulled back down the hill at 35 km/h through its original level. (The time required for the cart's reversal at the top of its climb is negligible.) What is the average speed of the cart for its round trip, from its original level back to its original level?
|  | |
| 101
In 1889, at Jubbulpore, India, a tug-of-war was finally won after 2 h 41 min, with the winning team displacing the center of the rope 3.7 m. In centimeters per minute, what was the magnitude of the average velocity of that center point during the contest?
|  | |
| 102
On average, an eye blink lasts about 100 ms. How far does a MiG-25 “Foxbat” fighter travel during a pilot's blink if the plane's average velocity is 3400 km/h?
|  | |
| 103
When the legal speed limit for the New York Thruway was increased from 55 mi/h to 65 mi/h, how much time was saved by a motorist who drove the 700 km between the Buffalo entrance and the New York City exit at the legal speed limit?
|  | |
| 104
A motorcycle is moving at 30 m/s when the rider applies the brakes, giving the motorcycle a constant deceleration. During the 3.0 s interval immediately after braking begins, the speed decreases to 15 m/s. What distance does the motorcycle travel from the instant braking begins until the motorcycle stops?
|  | |
| 105
A parachutist bails out and freely falls 50 m. Then the parachute opens, and thereafter she decelerates at 2.0 m/s2. She reaches the ground with a speed of 3.0 m/s. (a) How long is the parachutist in the air? (b) At what height does the fall begin?
|  | |
106
A pilot flies horizontally at 1300 km/h, at height h = 35 m above initially level ground. However, at time t = 0, the pilot begins to fly over ground sloping upward at angle q = 4.3° (Figure 2-39). If the pilot does not change the airplane's heading, at what time t does the plane strike the ground?
 | | Fig. 2-39 Problem 106.
|
|  | |
| 107
When a driver brings a car to a stop by braking as hard as possible, the stopping distance can be regarded as the sum of a “reaction distance,” which is initial speed multiplied by the driver's reaction time, and a “braking distance,” which is the distance traveled during braking. The following table gives typical values. (a) What reaction time is the driver assumed to have? (b) What is the car's stopping distance if the initial speed is 25 m/s?
|  | |
| 108
A shuffleboard disk is accelerated at a constant rate from rest to a speed of 6.0 m/s over a 1.8 m distance by a player using a cue. At this point the disk loses contact with the cue and slows at a constant rate of 2.5 m/s2 until it stops. (a) How much time elapses from when the disk begins to accelerate until it stops? (b) What total distance does the disk travel?
|  | |
| 109
A motorcyclist who is moving along an x axis directed toward the east has an acceleration given by a = (6.1 - 1.2t) m/s2 for 0 ≤ t ≤ 6.0 s. At t = 0, the velocity and position of the cyclist are 2.7 m/s and 7.3 m. (a) What is the maximum speed achieved by the cyclist? (b) What total distance does the cyclist travel between t = 0 and 6.0 s?
|  | |
| 110
The head of a rattlesnake can accelerate at 50 m/s2 in striking a victim. If a car could do as well, how long would it take to reach a speed of 100 km/h from rest?
|  | |
| 111
A jumbo jet must reach a speed of 360 km/h on the runway for takeoff. What is the lowest constant acceleration needed for takeoff from a 1.80 km runway?
|  | |
| 112
An automobile driver increases the speed at a constant rate from 25 km/h to 55 km/h in 0.50 min. A bicycle rider speeds up at a constant rate from rest to 30 km/h in 0.50 min. What are the magnitudes of (a) the driver's acceleration and (b) the rider's acceleration?
|  | |
| 113
At a military drill team contest at Fort Meade, Maryland, the home team moves forward with a sequence of four rates, given here with their U.S. definitions: (1) quick time (120 steps per minute, 30 in. per step), (2) half-step in quick time (120 steps per minute, 15 in. per step), (3) double time (180 steps per minute, 36 in. per step), (4) half-step in double time (180 steps per minute, 18 in. per step). If the team moves at each rate for 5.0 s, (a) how far in meters does the team move during the sequence and (b) what is the magnitude of their average velocity in meters per second? If, instead, the team moves at each rate for a distance of 8.00 m, (c) how long does the sequence take and (d) what is the magnitude of their average velocity in meters per second?
|  | |
| 114
A motorcyclist starts from rest and accelerates along a horizontal straight track. Photogates are attached to six posts evenly spaced every 10.0 m along the track; the first post is at the starting point. The photogates on each post measure the time required by the motorcyclist to reach that post. The following table gives the results for one test. (a) Find an expression for the distance d to each post in terms of the time t to reach that post and the acceleration a of the motorcyclist (assumed constant). (b) Using the data of the table, graph d versus t2. (c) Using a linear regression fit of the data, find the magnitude of the acceleration of the motorcyclist.
|  | |
115
At the National Physical Laboratory in England, a measurement of the free-fall acceleration g was made by throwing a glass ball straight up in an evacuated tube and letting it return. Let DTL in Figure 2-40 be the time interval between the two passages of the ball across a certain lower level, DTU the time interval between the two passages across an upper level, and H the distance between the two levels. Show that
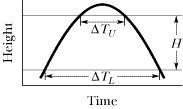 | | Fig. 2-40 Problem 115.
|
|  | |
| 116
The Zero Gravity Research Facility at the NASA Glenn Research Center includes a 145 m drop tower. This is an evacuated vertical tower through which, among other possibilities, a 1 m diameter sphere containing an experimental package can be dropped. (a) How long is the sphere in free fall? (b) What is its speed just as it reaches a catching device at the bottom of the tower? (c) When caught, the sphere experiences an average deceleration of 25g as its speed is reduced to zero. Through what distance does it travel during the deceleration?
|  | |
| 117
A ball is thrown down vertically with an initial speed of v0 from a height of h. (a) What is its speed just before it strikes the ground? (b) How long does the ball take to reach the ground? What would be the answers to (c) part a and (d) part b if the ball were thrown upward from the same height and with the same initial speed? Before solving any equations, decide whether the answers to (c) and (d) should be greater than, less than, or the same as in (a) and (b).
|  | |
On-Line Simulation Problems
The website http://www.wiley.com/college/halliday has simulation problems about this chapter.
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |