| CHAPTER 4 |
| Problems |
| ||||
| ||||
| ||||
| ||||||
| •1. |
A positron undergoes a displacement
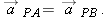 , ending with the position vector , ending with the position vector 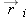 , in meters. What was the positron’s initial position vector? , in meters. What was the positron’s initial position vector? |
| •2. |
A watermelon seed has the following coordinates:
 , , 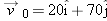 , and , and 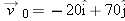 . Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction? . Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction? |
| •3. |
The position vector for an electron is
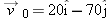 . (a) Find the magnitude of . (a) Find the magnitude of 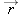 . (b) Sketch the vector on a right-handed coordinate system. . (b) Sketch the vector on a right-handed coordinate system. |
| ••4. |
The minute hand of a wall clock measures 10 cm from its tip to the axis about which it rotates. The magnitude and angle of the displacement vector of the tip are to be determined for three time intervals. What are the (a) magnitude and (b) angle from a quarter after the hour to half past, the (c) magnitude and (d) angle for the next half hour, and the (e) magnitude and (f) angle for the hour after that?
|
| |||||||||||||||||
| •5. |
An ion’s position vector is initially
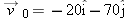 , and 10 s later it is , and 10 s later it is 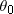 , all in meters. In unit-vector notation, what is its , all in meters. In unit-vector notation, what is its 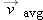 during the 10 s? during the 10 s? |
| •6. |
An electron’s position is given by
 , with t in seconds and , with t in seconds and 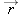 in meters. (a) In unit-vector notation, what is the electron’s velocity in meters. (a) In unit-vector notation, what is the electron’s velocity  ? At ? At 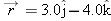 , what is , what is 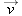 (b) in unit-vector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis? (b) in unit-vector notation and as (c) a magnitude and (d) an angle relative to the positive direction of the x axis? |
| •7. |
A train at a constant 60.0 km/h moves east for 40.0 min, then in a direction 50.0° east of due north for 20.0 min, and then west for 50.0 min. What are the (a) magnitude and (b) angle of its average velocity during this trip?
|
| |||||||||||||
| ••8. |
A plane flies 483 km east from city A to city B in 45.0 min and then 966 km south from city B to city C in 1.50 h. For the total trip, what are the (a) magnitude and (b) direction of the plane’s displacement, the (c) magnitude and (d) direction of its average velocity, and (e) its average speed?
|
| ••9. |
Figure 4-33 gives the path of a squirrel moving about on level ground, from point A (at time
 ), to points B (at ), to points B (at 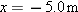 ), C (at ), C (at 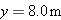 ), and finally D (at ), and finally D (at 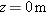 ). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the (c) magnitude and (d) angle of the one with the greatest magnitude? ). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the (c) magnitude and (d) angle of the one with the greatest magnitude?
|
| •••10. |
The position vector
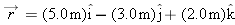 locates a particle as a function of time t. Vector locates a particle as a function of time t. Vector 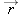 is in meters, t is in seconds, and factors e and f are constants. Figure 4-34 gives the angle is in meters, t is in seconds, and factors e and f are constants. Figure 4-34 gives the angle  of the particle’s direction of travel as a function of t ( of the particle’s direction of travel as a function of t ( is measured from the positive x direction). What are (a) e and (b) f, including units? is measured from the positive x direction). What are (a) e and (b) f, including units?
|
| ||||||||||||||||||
| •11. |
A particle moves so that its position (in meters) as a function of time (in seconds) is
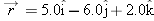 . Write expressions for (a) its velocity and (b) its acceleration as functions of time. . Write expressions for (a) its velocity and (b) its acceleration as functions of time. |
| |||||||||||||
| •12. |
A proton initially has
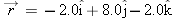 and then 4.0 s later has and then 4.0 s later has 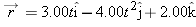 (in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration (in meters per second). For that 4.0 s, what are (a) the proton’s average acceleration  in unit-vector notation, (b) the magnitude of in unit-vector notation, (b) the magnitude of  , and (c) the angle between , and (c) the angle between 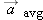 and the positive direction of the x axis? and the positive direction of the x axis? |
| •13. |
The position
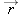 of a particle moving in an xy plane is given by of a particle moving in an xy plane is given by 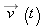 , with , with 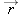 in meters and t in seconds. In unit-vector notation, calculate (a) in meters and t in seconds. In unit-vector notation, calculate (a) 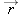 , (b) , (b) 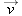 , and (c) , and (c)  for for 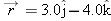 . (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at . (d) What is the angle between the positive direction of the x axis and a line tangent to the particle’s path at 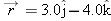 ? ?  |
| •14. |
At one instant a bicyclist is 40.0 m due east of a park’s flagpole, going due south with a speed of 10.0 m/s. Then 30.0 s later, the cyclist is 40.0 m due north of the flagpole, going due east with a speed of 10.0 m/s. For the cyclist in this 30.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the (c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration?
|
| ••15. |
A cart is propelled over an xy plane with acceleration components
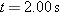 and and 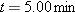 . Its initial velocity has components . Its initial velocity has components 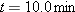 and and 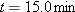 . In unit-vector notation, what is the velocity of the cart when it reaches its greatest y coordinate? . In unit-vector notation, what is the velocity of the cart when it reaches its greatest y coordinate? |
| ••16. |
A moderate wind accelerates a pebble over a horizontal xy plane with a constant acceleration
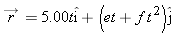 . At time . At time  , the velocity is , the velocity is 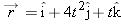 . What are the (a) magnitude and (b) angle of its velocity when it has been displaced by 12.0 m parallel to the x axis? . What are the (a) magnitude and (b) angle of its velocity when it has been displaced by 12.0 m parallel to the x axis? |
| ••17. |
A particle leaves the origin with an initial velocity
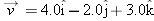 and a constant acceleration and a constant acceleration  . When it reaches its maximum x coordinate, what are its (a) velocity and (b) position vector? . When it reaches its maximum x coordinate, what are its (a) velocity and (b) position vector? |
| ||||||||||||||||
| ••18. |
The velocity
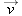 of a particle moving in the xy plane is given by of a particle moving in the xy plane is given by 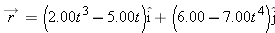 , with , with 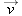 in meters per second and t (> 0) in seconds. (a) What is the acceleration when in meters per second and t (> 0) in seconds. (a) What is the acceleration when  ? (b) When (if ever) is the acceleration zero? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s? ? (b) When (if ever) is the acceleration zero? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s? |
| •••19. |
The acceleration of a particle moving only on a horizontal xy plane is given by
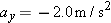 , where , where  is in meters per second-squared and t is in seconds. At is in meters per second-squared and t is in seconds. At  , the position vector , the position vector 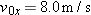 locates the paticle, which then has the velocity vector locates the paticle, which then has the velocity vector 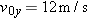 . At . At 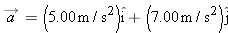 , what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis? , what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis? |
| •••20. |
In Fig. 4-35, particle A moves along the line
 with a constant velocity with a constant velocity 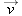 of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with zero initial speed and constant acceleration of magnitude 3.0 m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with zero initial speed and constant acceleration  of magnitude of magnitude 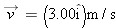 . What angle . What angle 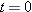 between between  and the positive direction of the y axis would result in a collision? and the positive direction of the y axis would result in a collision?
|
| ||||||||||||||||||||||||||||||
| •21. |
A projectile is fired horizontally from a gun that is 45.0 m above flat ground, emerging from the gun with a speed of 250 m/s. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does it strike the ground? (c) What is the magnitude of the vertical component of its velocity as it strikes the ground?
|
| •22. |
In the 1991 World Track and Field Championships in Tokyo, Mike Powell jumped 8.95 m, breaking by a full 5 cm the 23-year long-jump record set by Bob Beamon. Assume that Powell’s speed on takeoff was 9.5 m/s (about equal to that of a sprinter) and that
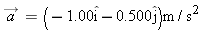 in Tokyo. How much less was Powell’s range than the maximum possible range for a particle launched at the same speed? in Tokyo. How much less was Powell’s range than the maximum possible range for a particle launched at the same speed?
|
| •23. |
The current world-record motorcycle jump is 77.0 m, set by Jason Renie. Assume that he left the take-off ramp at 12.0° to the horizontal and that the take-off and landing heights are the same. Neglecting air drag, determine his take-off speed.
|
| •24. |
A small ball rolls horizontally off the edge of a tabletop that is 1.20 m high. It strikes the floor at a point 1.52 m horizontally from the table edge. (a) How long is the ball in the air? (b) What is its speed at the instant it leaves the table?
|
| •25. |
A dart is thrown horizontally with an initial speed of 10 m/s toward point P, the bull’s-eye on a dart board. It hits at point Q on the rim, vertically below P, 0.19 s later. (a) What is the distance PQ? (b) How far away from the dart board is the dart released?
|
| •26. |
In Fig. 4-36, a stone is projected at a cliff of height h with an initial speed of 42.0 m/s directed at angle
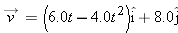 above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground. above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and (c) the maximum height H reached above the ground.
|
| •27. |
A certain airplane has a speed of 290.0 km/h and is diving at an angle of
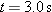 below the horizontal when the pilot releases a radar decoy (Fig. 4-37).The horizontal distance between the release point and the point where the decoy strikes the ground below the horizontal when the pilot releases a radar decoy (Fig. 4-37).The horizontal distance between the release point and the point where the decoy strikes the ground 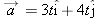 . (a) How long is the decoy in the air? (b) How high was the release point? . (a) How long is the decoy in the air? (b) How high was the release point?
|
| ||||||||||||||||||||||||||||
| •28. |
A stone is catapulted at time
 , with an initial velocity of magnitude 20.0 m/s and at an angle of 40.0° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at , with an initial velocity of magnitude 20.0 m/s and at an angle of 40.0° above the horizontal. What are the magnitudes of the (a) horizontal and (b) vertical components of its displacement from the catapult site at 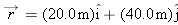 ? Repeat for the (c) horizontal and (d) vertical components at ? Repeat for the (c) horizontal and (d) vertical components at  , and for the (e) horizontal and (f) vertical components at , and for the (e) horizontal and (f) vertical components at  . . |
| ••29. |
A lowly high diver pushes off horizontally with a speed of 2.00 m/s from the platform edge 10.0 m above the surface of the water. (a) At what horizontal distance from the edge is the diver 0.800 s after pushing off? (b) At what vertical distance above the surface of the water is the diver just then? (c) At what horizontal distance from the edge does the diver strike the water?
|
| |||||||||||||
| ••30. |
A trebuchet was a hurling machine built to attack the walls of a castle under siege. A large stone could be hurled against a wall to break apart the wall. The machine was not placed near the wall because then arrows could reach it from the castle wall. Instead, it was positioned so that the stone hit the wall during the second half of its flight. Suppose a stone is launched with a speed of
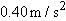 and at an angle of and at an angle of 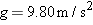 . What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)? . What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?
|
| ••31. |
A plane, diving with constant speed at an angle of 53.0° with the vertical, releases a projectile at an altitude of 730 m. The projectile hits the ground 5.00 s after release. (a) What is the speed of the plane? (b) How far does the projectile travel horizontally during its flight? What are the (c) horizontal and (d) vertical components of its velocity just before striking the ground?
|
| |||||||||||||
| ••32. |
During a tennis match, a player serves the ball at 23.6 m/s, with the center of the ball leaving the racquet horizontally 2.37 m above the court surface. The net is 12 m away and 0.90 m high. When the ball reaches the net, (a) does the ball clear it and (b) what is the distance between the center of the ball and the top of the net? Suppose that, instead, the ball is served as before but now it leaves the racquet at 5.00° below the horizontal. When the ball reaches the net, (c) does the ball clear it and (d) what now is the distance between the center of the ball and the top of the net?
|
| ••33. |
In a jump spike, a volleyball player slams the ball from overhead and toward the opposite floor. Controlling the angle of the spike is difficult. Suppose a ball is spiked from a height of 2.30 m with an initial speed of 20.0 m/s at a downward angle of 18.00°. How much farther on the opposite floor would it have landed if the downward angle were, instead, 8.00°?
|
| ••34. |
A soccer ball is kicked from the ground with an initial speed of 19.5 m/s at an upward angle of 45°. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to meet the ball just before it hits the ground?
|
| ••35. |
A projectile’s launch speed is five times its speed at maximum height. Find launch angle
 . . |
| ••36. |
Suppose that a shot putter can put a shot at the world-class speed
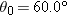 and at a height of 2.160 m. What horizontal distance would the shot travel if the launch angle and at a height of 2.160 m. What horizontal distance would the shot travel if the launch angle  is (a) 45.00° and (b) 42.00°? The answers indicate that the angle of 45°, which maximizes the range of projectile motion, does not maximize the horizontal distance when the launch and landing are at different heights. is (a) 45.00° and (b) 42.00°? The answers indicate that the angle of 45°, which maximizes the range of projectile motion, does not maximize the horizontal distance when the launch and landing are at different heights.
|
| ••37. |
A ball is shot from the ground into the air. At a height of 9.1 m, its velocity is
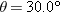 , with , with 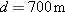 horizontal and horizontal and 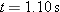 upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball’s velocity just before it hits the ground? upward. (a) To what maximum height does the ball rise? (b) What total horizontal distance does the ball travel? What are the (c) magnitude and (d) angle (below the horizontal) of the ball’s velocity just before it hits the ground? |
| |||||||||||||
| ••38. |
You throw a ball toward a wall at speed 25.0 m/s and at angle
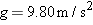 above the horizontal (Fig. 4-38). The wall is distance above the horizontal (Fig. 4-38). The wall is distance  from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory? from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?
|
| ••39. |
A rifle that shoots bullets at 460 m/s is to be aimed at a target 45.7 m away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
|
| |||||||||||||
| ••40. |
A baseball leaves a pitcher’s hand horizontally at a speed of 161 km/h. The distance to the batter is 18.3 m. (a) How long does the ball take to travel the first half of that distance? (b) The second half? (c) How far does the ball fall freely during the first half? (d) During the second half? (e) Why aren’t the quantities in (c) and (d) equal?
|
| ••41. |
In Fig. 4-39, a ball is thrown leftward from the left edge of the roof, at height h above the ground. The ball hits the ground 1.50 s later, at distance
 from the building and at angle from the building and at angle 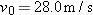 with the horizontal. (a) Find h (Hint: One way is to reverse the motion, as if on videotape.) What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal? with the horizontal. (a) Find h (Hint: One way is to reverse the motion, as if on videotape.) What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal?
|
| ••42. |
A golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in Fig. 4-40, where
 at the instant the ball is struck. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball? at the instant the ball is struck. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball?
|
| ••43. |
In Fig. 4-41, a ball is launched with a velocity of magnitude 10.0 m/s, at an angle of 50.0° to the horizontal. The launch point is at the base of a ramp of horizontal length
 and height and height 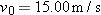 . A plateau is located at the top of the ramp. (a) Does the ball land on the ramp or the plateau? When it lands, what are the (b) magnitude and (c) angle of its displacement from the launch point? . A plateau is located at the top of the ramp. (a) Does the ball land on the ramp or the plateau? When it lands, what are the (b) magnitude and (c) angle of its displacement from the launch point?
|
| ••44. |
In 1939 or 1940, Emanuel Zacchini took his human-cannonball act to an extreme: After being shot from a cannon, he soared over three Ferris wheels and into a net (Fig. 4-42). (a) Treating him as a particle, calculate his clearance over the first wheel. (b) If he reached maximum height over the middle wheel, by how much did he clear it? (c) How far from the cannon should the net’s center have been positioned (neglect air drag)?
|
| ••45. |
Upon spotting an insect on a twig overhanging water, an archer fish squirts water drops at the insect to knock it into the water (Fig. 4-43). Although the fish sees the insect along a straight-line path at angle
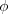 and distance d, a drop must be launched at a different angle and distance d, a drop must be launched at a different angle  if its parabolic path is to intersect the insect. If if its parabolic path is to intersect the insect. If 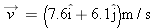 , , 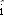 , and the launch speed is 3.56 m/s, what , and the launch speed is 3.56 m/s, what  is required for the drop to be at the top of the parabolic path when it reaches the insect? is required for the drop to be at the top of the parabolic path when it reaches the insect?
|
| ••46. |
In Fig. 4-44, a ball is thrown up onto a roof, landing 4.00 s later at height
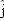 above the release level. The ball’s path just before landing is angled at above the release level. The ball’s path just before landing is angled at 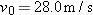 with the roof. (a) Find the horizontal distance d it travels. (See the hint to Problem 41.) What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity? with the roof. (a) Find the horizontal distance d it travels. (See the hint to Problem 41.) What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity?
|
| ••47. |
A batter hits a pitched ball when the center of the ball is 1.22 m above the ground. The ball leaves the bat at an angle of 45° with the ground. With that launch, the ball should have a horizontal range (returning to the launch level) of 107 m. (a) Does the ball clear a 7.32-m-high fence that is 97.5 m horizontally from the launch point? (b) At the fence, what is the distance between the fence top and the ball center?
|
| |||||||||||||
| ••48. |
In basketball, hang is an illusion in which a player seems to weaken the gravitational acceleration while in midair. The illusion depends much on a skilled player’s ability to rapidly shift the ball between hands during the flight, but it might also be supported by the longer horizontal distance the player travels in the upper part of the jump than in the lower part. If a player jumps with an initial speed of
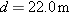 at an angle of at an angle of 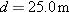 , what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)? , what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)?
|
| •••49. |
A skilled skier knows to jump upward before reaching a downward slope. Consider a jump in which the launch speed is
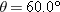 , the launch angle is , the launch angle is  , the initial course is approximately flat, and the steeper track has a slope of 11.3°. Figure 4-45a shows a prejump that allows the skier to land on the top portion of the steeper track. Figure 4-45b shows a jump at the edge of the steeper track. In Fig. 4-45a, the skier lands at approximately the launch level, (a) In the landing, what is the angle , the initial course is approximately flat, and the steeper track has a slope of 11.3°. Figure 4-45a shows a prejump that allows the skier to land on the top portion of the steeper track. Figure 4-45b shows a jump at the edge of the steeper track. In Fig. 4-45a, the skier lands at approximately the launch level, (a) In the landing, what is the angle 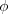 between the skier’s path and the slope? In Fig. 4-45b, (b) how far below the launch level does the skier land and (c) what is between the skier’s path and the slope? In Fig. 4-45b, (b) how far below the launch level does the skier land and (c) what is 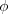 ? (The greater fall and greater ? (The greater fall and greater 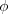 can result in loss of control in the landing.) can result in loss of control in the landing.)
|
| •••50. |
| •••51. |
A football kicker can give the ball an initial speed of 25 m/s. What are the (a) least and (b) greatest elevation angles at which he can kick the ball to score a field goal from a point 50 m in front of goalposts whose horizontal bar is 3.44 m above the ground?
|
| |||||||||||||
| •••52. |
A ball is to be shot from level ground with a certain speed. Figure 4-47 shows the range R it will have versus the launch angle
 . The value of . The value of  determines the flight time; let determines the flight time; let 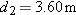 represent the maximum flight time. What is the least speed the ball will have during its flight if represent the maximum flight time. What is the least speed the ball will have during its flight if  is chosen such that the flight time is is chosen such that the flight time is 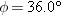 ? ?
|
| •••53. |
A ball rolls horizontally off the top of a stairway with a speed of 1.52 m/s. The steps are 20.3 cm high and 20.3 cm wide. Which step does the ball hit first?
|
| |||||||||||||
| •••54. |
Two seconds after being projected from ground level, a projectile is displaced 40 m horizontally and 53 m vertically above its launch point. What are the (a) horizontal and (b) vertical components of the initial velocity of the projectile? (c) At the instant the projectile achieves its maximum height above ground level, how far is it displaced horizontally from the launch point?
 |
| •••55. |
In Fig. 4-48, a baseball is hit at a height
 and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance 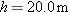 farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall? farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall?
|
| |||||||||||||||
| •56. |
A centripetal-acceleration addict rides in uniform circular motion with period
 and radius and radius 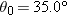 . At . At 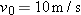 his acceleration is his acceleration is 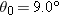 . At that instant, what are the values of (a) . At that instant, what are the values of (a)  and (b) and (b) 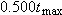 ? ? |
| •57. |
A woman rides a carnival Ferris wheel at radius 15 m, completing five turns about its horizontal axis every minute. What are (a) the period of the motion, the (b) magnitude and (c) direction of her centripetal acceleration at the highest point, and the (d) magnitude and (e) direction of her centripetal acceleration at the lowest point?
|
| |||||||||||||
| •58. |
What is the magnitude of the acceleration of a sprinter running at 10 m/s when rounding a turn of a radius 25 m?
|
| •59. |
When a large star becomes a supernova, its core may be compressed so tightly that it becomes a neutron star, with a radius of about 20 km (about the size of the San Francisco area). If a neutron star rotates once every second, (a) what is the speed of a particle on the star’s equator and (b) what is the magnitude of the particle’s centripetal acceleration? (c) If the neutron star rotates faster, do the answers to (a) and (b) increase, decrease, or remain the same?
|
| •60. |
An Earth satellite moves in a circular orbit 640 km above Earth’s surface with a period of 98.0 min. What are the (a) speed and (b) magnitude of the centripetal acceleration of the satellite?
|
| •61. |
A carnival merry-go-round rotates about a vertical axis at a constant rate. A man standing on the edge has a constant speed of 3.66 m/s and a centripetal acceleration
 of magnitude of magnitude  . Position vector . Position vector 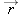 locates him relative to the rotation axis. (a) What is the magnitude of locates him relative to the rotation axis. (a) What is the magnitude of 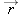 ? What is the direction of ? What is the direction of 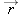 when when  is directed (b) due east and (c) due south? is directed (b) due east and (c) due south? |
| •62. |
A rotating fan completes 1200 revolutions every minute. Consider the tip of a blade, at a radius of 0.15 m. (a) Through what distance does the tip move in one revolution? What are (b) the tip’s speed and (c) the magnitude of its acceleration? (d) What is the period of the motion?
|
| ••63. |
A purse at radius 2.00 m and a wallet at radius 3.00 m travel in uniform circular motion on the floor of a merry-go-round as the ride turns. They are on the same radial line. At one instant, the acceleration of the purse is
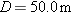 . At that instant and in unit-vector notation, what is the acceleration of the wallet? . At that instant and in unit-vector notation, what is the acceleration of the wallet? |
| ••64. |
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time
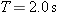 , it is at point (5.00 m, 6.00 m) with velocity , it is at point (5.00 m, 6.00 m) with velocity 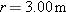 and acceleration in the positive x direction. At time and acceleration in the positive x direction. At time  , it has velocity , it has velocity 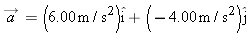 and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if  is less than one period? is less than one period? |
| ••65. |
At
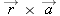 , the acceleration of a particle in counterclockwise circular motion is , the acceleration of a particle in counterclockwise circular motion is 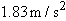 . It moves at constant speed. At time . It moves at constant speed. At time 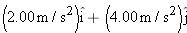 , its acceleration is , its acceleration is 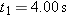 . What is the radius of the path taken by the particle if . What is the radius of the path taken by the particle if  is less than one period? is less than one period?  |
| ••66. |
A particle moves horizontally in uniform circular motion, over a horizontal xy plane. At one instant, it moves through the point at coordinates (4.00 m, 4.00 m) with a velocity of
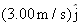 and an acceleration of and an acceleration of 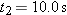 . What are the (a) x and (b) y coordinates of the center of the circular path? . What are the (a) x and (b) y coordinates of the center of the circular path? |
| •••67. |
A boy whirls a stone in a horizontal circle of radius 1.5 m and at height 2.0 m above level ground. The string breaks, and the stone flies off horizontally and strikes the ground after traveling a horizontal distance of 10 m. What is the magnitude of the centripetal acceleration of the stone during the circular motion?
|
| |||||||||||||
| •••68. |
A cat rides a merry-go-round turning with uniform circular motion. At time
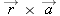 , the cat’s velocity is , the cat’s velocity is 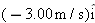 , measured on a horizontal xy coordinate system. At , measured on a horizontal xy coordinate system. At 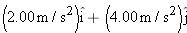 , its velocity is , its velocity is 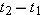 . What are (a) the magnitude of the cat’s centripetal acceleration and (b) the cat’s average acceleration during the time interval . What are (a) the magnitude of the cat’s centripetal acceleration and (b) the cat’s average acceleration during the time interval  , which is less than one period? , which is less than one period? |
| ||||||
| •69. |
A cameraman on a pickup truck is traveling westward at 20 km/h while he videotapes a cheetah that is moving westward 30 km/h faster than the truck. Suddenly, the cheetah stops, turns, and then runs at 45 km/h eastward, as measured by a suddenly nervous crew member who stands alongside the cheetah’s path. The change in the animal’s velocity takes 2.0 s. What are the (a) magnitude and (b) direction of the animal’s acceleration according to the cameraman and the (c) magnitude and (d) direction according to the nervous crew member?
|
| •70. |
A boat is traveling upstream in the positive direction of an x axis at 14 km/h with respect to the water of a river. The water is flowing at 9.0 km/h with respect to the ground. What are the (a) magnitude and (b) direction of the boat’s velocity with respect to the ground? A child on the boat walks from front to rear at 6.0 km/h with respect to the boat. What are the (c) magnitude and (d) direction of the child’s velocity with respect to the ground?
|
| ••71. |
A suspicious-looking man runs as fast as he can along a moving sidewalk from one end to the other, taking 2.50 s. Then security agents appear, and the man runs as fast as he can back along the sidewalk to his starting point, taking 10.0 s. What is the ratio of the man’s running speed to the sidewalk’s speed?
|
| ||||||||||||||||||
| •72. |
A rugby player runs with the ball directly toward his opponent’s goal, along the positive direction of an x axis. He can legally pass the ball to a teammate as long as the ball’s velocity relative to the field does not have a positive x component. Suppose the player runs at speed 4.0 m/s relative to the field while he passes the ball with velocity
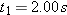 relative to himself. If relative to himself. If 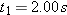 has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal? has magnitude 6.0 m/s, what is the smallest angle it can have for the pass to be legal? |
| ••73. |
Two ships, A and B, leave port at the same time. Ship A travels northwest at 24 knots, and ship B travels at 28 knots in a direction 40° west of south. (1 knot = 1 nautical mile per hour; see Appendix D.) What are the (a) magnitude and (b) direction of the velocity of ship A relative to B? (c) After what time will the ships be 160 nautical miles apart? (d) What will be the bearing of B (the direction of B’s position) relative to A at that time?
|
| ||||||||||||||||
| ••74. |
A light plane attains an airspeed of 500 km/h.The pilot sets out for a destination 800 km due north but discovers that the plane must be headed 20.0° east of due north to fly there directly. The plane arrives in 2.00 h. What were the (a) magnitude and (b) direction of the wind velocity?
|
| ••75. |
Snow is falling vertically at a constant speed of 8.0 m/s. At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car traveling on a straight, level road with a speed of 50 km/h?
|
| |||||||||||||
| ••76. |
After flying for 15 min in a wind blowing 42 km/h at an angle of 20° south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
|
| ••77. |
A train travels due south at 30 m/s (relative to the ground) in a rain that is blown toward the south by the wind. The path of each raindrop makes an angle of 70° with the vertical, as measured by an observer stationary on the ground. An observer on the train, however, sees the drops fall perfectly vertically. Determine the speed of the raindrops relative to the ground.
|
| |||||||||||||
| ••78. |
A 200-m-wide river flows due east at a uniform speed of 2.0 m/s. A boat with a speed of 8.0 m/s relative to the water leaves the south bank pointed in a direction 30° west of north. What are the (a) magnitude and (b) direction of the boat’s velocity relative to the ground? (c) How long does the boat take to cross the river?
 |
| ••79. |
Two highways intersect as shown in Fig. 4-49. At the instant shown, a police car P is distance
 from the intersection and moving at speed from the intersection and moving at speed 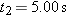 . Motorist M is distance . Motorist M is distance 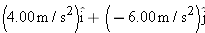 from the intersection and moving at speed from the intersection and moving at speed 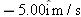 . (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-49, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection? . (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-49, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection?
|
| ••80. |
In the overhead view of Fig. 4-50, Jeeps P and B race along straight lines, across flat terrain, and past stationary border guard A. Relative to the guard, B travels at a constant speed of 20.0 m/s, at the angle
 . Relative to the guard, P has accelerated from rest at a constant rate of . Relative to the guard, P has accelerated from rest at a constant rate of 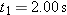 at the angle at the angle 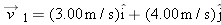 . At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the (c) magnitude and (d) direction of the acceleration of P relative to B? . At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the (c) magnitude and (d) direction of the acceleration of P relative to B?
|
| •••81. |
Ship A is located 4.0 km north and 2.5 km east of ship B. Ship A has a velocity of 22 km/h toward the south, and ship B has a velocity of 40 km/h in a direction 37° north of east. (a) What is the velocity of A relative to B in unit-vector notation with
 toward the east? (b) Write an expression (in terms of toward the east? (b) Write an expression (in terms of  and and 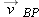 ) for the position of A relative to B as a function of t, where ) for the position of A relative to B as a function of t, where  when the ships are in the positions described above. (c) At what time is the separation between the ships least? (d) What is that least separation? when the ships are in the positions described above. (c) At what time is the separation between the ships least? (d) What is that least separation? |
| •••82. |
A 200-m-wide river has a uniform flow speed of 1.1 m/s through a jungle and toward the east. An explorer wishes to leave a small clearing on the south bank and cross the river in a powerboat that moves at a constant speed of 4.0 m/s with respect to the water. There is a clearing on the north bank 82 m upstream from a point directly opposite the clearing on the south bank. (a) In what direction must the boat be pointed in order to travel in a straight line and land in the clearing on the north bank? (b) How long will the boat take to cross the river and land in the clearing?
|
| 83. |
You are kidnapped by political-science majors (who are upset because you told them political science is not a real science). Although blindfolded, you can tell the speed of their car (by the whine of the engine), the time of travel (by mentally counting off seconds), and the direction of travel (by turns along the rectangular street system). From these clues, you know that you are taken along the following course: 50 km/h for 2.0 min, turn 90° to the right, 20 km/h for 4.0 min, turn 90° to the right, 20 km/h for 60 s, turn 90° to the left, 50 km/h for 60 s, turn 90° to the right, 20 km/h for 2.0 min, turn 90° to the left, 50 km/h for 30 s. At that point, (a) how far are you from your starting point, and (b) in what direction relative to your initial direction of travel are you?
|
| 84. |
Curtain of death. A large metallic asteroid strikes Earth and quickly digs a crater into the rocky material below ground level by launching rocks upward and outward. The following table gives five pairs of launch speeds and angles (from the horizontal) for such rocks, based on a model of crater formation. (Other rocks, with intermediate speeds and angles, are also launched.) Suppose that you are at
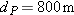 when the asteroid strikes the ground at time when the asteroid strikes the ground at time  and position and position 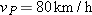 (Fig. 4-51). (a) At (Fig. 4-51). (a) At 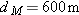 , what are the x and y coordinates of the rocks headed in your direction from launches A through E? (b) Plot these coordinates and then sketch a curve through the points to include rocks with intermediate launch speeds and angles. The curve should indicate what you would see as you look up into the approaching rocks and what dinosaurs must have seen during asteroid strikes long ago. , what are the x and y coordinates of the rocks headed in your direction from launches A through E? (b) Plot these coordinates and then sketch a curve through the points to include rocks with intermediate launch speeds and angles. The curve should indicate what you would see as you look up into the approaching rocks and what dinosaurs must have seen during asteroid strikes long ago.
|
| 85. |
In Fig. 4-52, a lump of wet putty moves in uniform circular motion as it rides at a radius of 20.0 cm on the rim of a wheel rotating counterclock wise with a period of 5.00 ms. The lump then happens to fly off the rim at the 5 o’clock position (as if on a clock face). It leaves the rim at a height of
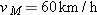 from the floor and at a distance from the floor and at a distance 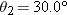 from a wall. At what height on the wall does the lump hit? from a wall. At what height on the wall does the lump hit?
|
| 86. |
A particle is in uniform circular motion about the origin of an xy coordinate system, moving clockwise with a period of 7.00 s. At one instant, its position vector (from the origin) is
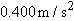 . At that instant, what is its velocity in unit-vector notation? . At that instant, what is its velocity in unit-vector notation? |
| 87. |
In Fig. 4-53, a ball is shot directly upward from the ground with an initial speed of
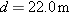 . Simultaneously, a construction elevator cab begins to move upward from the ground with a constant speed of . Simultaneously, a construction elevator cab begins to move upward from the ground with a constant speed of  . What maximum height does the ball reach relative to (a) the ground and (b) the cab floor? At what rate does the speed of the ball change relative to (c) the ground and (d) the cab floor? . What maximum height does the ball reach relative to (a) the ground and (b) the cab floor? At what rate does the speed of the ball change relative to (c) the ground and (d) the cab floor?
|
| 88. |
In Fig. 4-54a, a sled moves in the negative x direction at constant speed
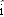 while a ball of ice is shot from the sled with a velocity while a ball of ice is shot from the sled with a velocity 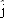 relative to the sled. When the ball lands, its horizontal displacement relative to the sled. When the ball lands, its horizontal displacement 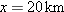 relative to the ground (from its launch position to its landing position) is measured. Figure 4-54b gives relative to the ground (from its launch position to its landing position) is measured. Figure 4-54b gives 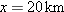 as a function of as a function of 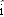 . Assume the ball lands at approximately its launch height. What are the values of (a) . Assume the ball lands at approximately its launch height. What are the values of (a) 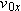 and (b) and (b)  ? The ball’s displacement ? The ball’s displacement 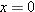 relative to the sled can also be measured. Assume that the sled’s velocity is not changed when the ball is shot. What is relative to the sled can also be measured. Assume that the sled’s velocity is not changed when the ball is shot. What is 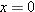 when when 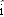 is (c) 5.0 m/s and (d) 15 m/s? is (c) 5.0 m/s and (d) 15 m/s?
|
| 89. |
A woman who can row a boat at 6.4 km/h in still water faces a long, straight river with a width of 6.4 km and a current of 3.2 km/h. Let
 point directly across the river and point directly across the river and 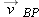 point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to point directly downstream. If she rows in a straight line to a point directly opposite her starting position, (a) at what angle to  must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows 3.2 km down the river and then back to her starting point? (d) How long if she rows 3.2 km up the river and then back to her starting point? (e) At what angle to must she point the boat and (b) how long will she take? (c) How long will she take if, instead, she rows 3.2 km down the river and then back to her starting point? (d) How long if she rows 3.2 km up the river and then back to her starting point? (e) At what angle to  should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time? should she point the boat if she wants to cross the river in the shortest possible time? (f) How long is that shortest time? |
| 90. |
In Fig. 4-55, a radar station detects an airplane approach ing directly from the east. At first observation, the airplane is at distance
 from the station and at angle from the station and at angle 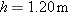 above the horizon. The airplane is tracked through an angular change above the horizon. The airplane is tracked through an angular change 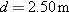 in the vertical east–west plane; its distance is then in the vertical east–west plane; its distance is then  . Find the (a) magnitude and (b) direction of the airplane’s displacement during this period. . Find the (a) magnitude and (b) direction of the airplane’s displacement during this period.
|
| 91. |
A rifle is aimed horizontally at a target 30 m away. The bullet hits the target 1.9 cm below the aiming point. What are (a) the bullet’s time of flight and (b) its speed as it emerges from the rifle?
|
| |||||||||||||
| 92. |
The fast French train known as the TGV (Train à Grande Vitesse) has a scheduled average speed of 216 km/h. (a) If the train goes around a curve at that speed and the magnitude of the acceleration experienced by the passengers is to be limited to 0.050g, what is the smallest radius of curvature for the track that can be tolerated? (b) At what speed must the train go around a curve with a 1.00 km radius to be at the acceleration limit?
|
| 93. |
A magnetic field can force a charged particle to move in a circular path. Suppose that an electron moving in a circle experiences a radial acceleration of magnitude
 in a particular magnetic field. (a) What is the speed of the electron if the radius of its circular path is 15 cm? (b) What is the period of the motion? in a particular magnetic field. (a) What is the speed of the electron if the radius of its circular path is 15 cm? (b) What is the period of the motion? |
| 94. |
The position vector for a proton is initially
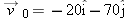 and then later is and then later is 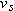 , all in meters. (a) What is the proton’s displacement vector, and (b) to what plane is that vector parallel? , all in meters. (a) What is the proton’s displacement vector, and (b) to what plane is that vector parallel? |
| 95. |
A particle P travels with constant speed on a circle of radius 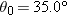 (Fig. 4-56) and completes one revolution in 20.0 s. The particle passes through O at time (Fig. 4-56) and completes one revolution in 20.0 s. The particle passes through O at time  . State the following vectors in magnitude-angle notation (angle relative to the positive direction of x). With respect to O, find the particle’s position vector at the times t of (a) 5.00 s, (b) 7.50 s, and (c) 10.0 s. . State the following vectors in magnitude-angle notation (angle relative to the positive direction of x). With respect to O, find the particle’s position vector at the times t of (a) 5.00 s, (b) 7.50 s, and (c) 10.0 s.(d) For the 5.00 s interval from the end of the fifth second to the end of the tenth second, find the particle’s displacement. For that interval, find (e) its average velocity and its velocity at the (f) beginning and (g) end. Next, find the acceleration at the (h) beginning and (i) end of that interval.
|
| 96. |
An iceboat sails across the surface of a frozen lake with constant acceleration produced by the wind. At a certain instant the boat’s velocity is
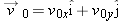 . Three seconds later, because of a wind shift, the boat is instantaneously at rest. What is its average acceleration for this 3 s interval? . Three seconds later, because of a wind shift, the boat is instantaneously at rest. What is its average acceleration for this 3 s interval? |
| 97. |
In 3.50 h, a balloon drifts 21.5 km north, 9.70 km east, and 2.88 km upward from its release point on the ground. Find (a) the magnitude of its average velocity and (b) the angle its average velocity makes with the horizontal.
|
| 98. |
A ball is thrown horizontally from a height of 20 m and hits the ground with a speed that is three times its initial speed. What is the initial speed?
|
| 99. |
A projectile is launched with an initial speed of 30 m/s at an angle of 60° above the horizontal. What are the (a) magnitude and (b) angle of its velocity 2.0 s after launch, and (c) is the angle above or below the horizontal? What are the (d) magnitude and (e) angle of its velocity 5.0 s after launch, and (f) is the angle above or below the horizontal?
|
| 100. |
An airport terminal has a moving sidewalk to speed passengers through a long corridor. Larry does not use the moving sidewalk; he takes 150 s to walk through the corridor. Curly, who simply stands on the moving sidewalk, covers the same distance in 70 s. Moe boards the sidewalk and walks along it. How long does Moe take to move through the corridor? Assume that Larry and Moe walk at the same speed.
|
| 101. |
A football player punts the football so that it will have a “hang time” (time of flight) of 4.5 s and land 46 m away. If the ball leaves the player’s foot 150 cm above the ground, what must be the (a) magnitude and (b) angle (relative to the horizontal) of the ball’s initial velocity?
|
| 102. |
For women’s volleyball the top of the net is 2.24 m above the floor and the court measures 9.0 m by 9.0 m on each side of the net. Using a jump serve, a player strikes the ball at a point that is 3.0 m above the floor and a horizontal distance of 8.0 m from the net. If the initial velocity of the ball is horizontal, (a) what minimum magnitude must it have if the ball is to clear the net and (b) what maximum magnitude can it have if the ball is to strike the floor inside the back line on the other side of the net?
|
| 103. |
Figure 4-57 shows the straight path of a particle across an xy coordinate system as the particle is accelerated from rest during time interval
 . The acceleration is constant. The xy coordinates for point A are (4.00 m, 6.00 m); those for point B are (12.0 m, 18.0 m). (a) What is the ratio . The acceleration is constant. The xy coordinates for point A are (4.00 m, 6.00 m); those for point B are (12.0 m, 18.0 m). (a) What is the ratio 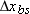 of the acceleration components? (b) What are the coordinates of the particle if the motion is continued for another interval equal to of the acceleration components? (b) What are the coordinates of the particle if the motion is continued for another interval equal to  ? ?
|
| 104. |
An astronaut is rotated in a horizontal centrifuge at a radius of 5.0 m. (a) What is the astronaut’s speed if the centripetal acceleration has a magnitude of 7.0g? (b) How many revolutions per minute are required to produce this acceleration? (c) What is the period of the motion?
|
| 105. |
(a) What is the magnitude of the centripetal acceleration of an object on Earth’s equator due to the rotation of Earth? (b) What would Earth’s rotation period have to be for objects on the equator to have a centripetal acceleration of magnitude
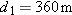 ? ? |
| 106. |
A person walks up a stalled 15-m-long escalator in 90 s. When standing on the same escalator, now moving, the person is carried up in 60 s. How much time would it take that person to walk up the moving escalator? Does the answer depend on the length of the escalator?
|
| 107. |
A baseball is hit at ground level. The ball reaches its maximum height above ground level 3.0 s after being hit. Then 2.5 s after reaching its maximum height, the ball barely clears a fence that is 97.5 m from where it was hit. Assume the ground is level. (a) What maximum height above ground level is reached by the ball? (b) How high is the fence? (c) How far beyond the fence does the ball strike the ground?
|
| |||||||||||||
| 108. |
The range of a projectile depends not only on
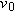 and and  but also on the value g of the free-fall acceleration, which varies from place to place. In 1936, Jesse Owens established a world’s running broad jump record of 8.09 m at the Olympic Games at Berlin (where but also on the value g of the free-fall acceleration, which varies from place to place. In 1936, Jesse Owens established a world’s running broad jump record of 8.09 m at the Olympic Games at Berlin (where 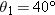 ). Assuming the same values of ). Assuming the same values of 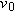 and and  , by how much would his record have differed if he had competed instead in 1956 at Melbourne (where , by how much would his record have differed if he had competed instead in 1956 at Melbourne (where 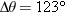 )? )? 
|
| 109. |
During volcanic eruptions, chunks of solid rock can be blasted out of the volcano; these projectiles are called volcanic bombs. Figure 4-58 shows a cross section of Mt. Fuji, in Japan. (a) At what initial speed would a bomb have to be ejected, at angle
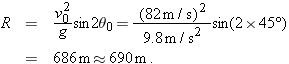 to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance 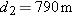 and horizontal distance and horizontal distance 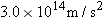 ? Ignore, for the moment, the effects of air on the bomb’s travel. (b) What would be the time of flight? (c) Would the effect of the air increase or decrease your answer in (a)? ? Ignore, for the moment, the effects of air on the bomb’s travel. (b) What would be the time of flight? (c) Would the effect of the air increase or decrease your answer in (a)?
|
| 110. |
Long flights at midlatitudes in the Northern Hemisphere encounter the jet stream, an eastward airflow that can affect a plane’s speed relative to Earth’s surface. If a pilot maintains a certain speed relative to the air (the plane’s airspeed), the speed relative to the surface (the plane’s ground speed) is more when the flight is in the direction of the jet stream and less when the flight is opposite the jet stream. Suppose a round-trip flight is scheduled between two cities separated by 4000 km, with the outgoing flight in the direction of the jet stream and the return flight opposite it. The airline computer advises an airspeed of 1000 km/h, for which the difference in flight times for the outgoing and return flights is 70.0 min. What jet-stream speed is the computer using?
|
| 111. |
A particle starts from the origin at
 with a velocity of with a velocity of 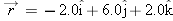 and moves in the xy plane with constant acceleration and moves in the xy plane with constant acceleration 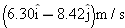 . When the particle’s x coordinate is 29 m, what are its (a) y coordinate and (b) speed? . When the particle’s x coordinate is 29 m, what are its (a) y coordinate and (b) speed? |
| |||||||||||||
| 112. |
A sprinter running on a circular track has a velocity of constant magnitude 9.2 m/s and a centripetal acceleration of magnitude
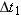 . What are (a) the track radius and (b) the period of the circular motion? . What are (a) the track radius and (b) the period of the circular motion? |
| 113. |
An electron having an initial horizontal velocity of magnitude
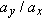 travels into the region between two horizontal metal plates that are electrically charged. In that region, the electron travels a horizontal distance of 2.00 cm and has a constant downward acceleration of magnitude travels into the region between two horizontal metal plates that are electrically charged. In that region, the electron travels a horizontal distance of 2.00 cm and has a constant downward acceleration of magnitude 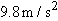 due to the charged plates. Find (a) the time the electron takes to travel the 2.00 cm, (b) the vertical distance it travels during that time, and the magnitudes of its (c) horizontal and (d) vertical velocity components as it emerges from the region. due to the charged plates. Find (a) the time the electron takes to travel the 2.00 cm, (b) the vertical distance it travels during that time, and the magnitudes of its (c) horizontal and (d) vertical velocity components as it emerges from the region. |
| 114. |
An elevator without a ceiling is ascending with a constant speed of 10 m/s. A boy on the elevator shoots a ball directly upward, from a height of 2.0 m above the elevator floor, just as the elevator floor is 28 m above the ground. The initial speed of the ball with respect to the elevator is 20 m/s. (a) What maximum height above the ground does the ball reach? (b) How long does the ball take to return to the elevator floor?
|
| 115. |
Suppose that a space probe can withstand the stresses of a 20g acceleration. (a) What is the minimum turning radius of such a craft moving at a speed of one-tenth the speed of light? (b) How long would it take to complete a 90° turn at this speed?
|
| 116. |
| 117. |
A wooden boxcar is moving along a straight railroad track at speed
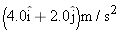 . A sniper fires a bullet (initial speed . A sniper fires a bullet (initial speed 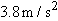 ) at it from a high-powered rifle. The bullet passes through both lengthwise walls of the car, its entrance and exit holes being exactly opposite each other as viewed from within the car. From what direction, relative to the track, is the bullet fired? Assume that the bullet is not deflected upon entering the car, but that its speed decreases by 20%.Take ) at it from a high-powered rifle. The bullet passes through both lengthwise walls of the car, its entrance and exit holes being exactly opposite each other as viewed from within the car. From what direction, relative to the track, is the bullet fired? Assume that the bullet is not deflected upon entering the car, but that its speed decreases by 20%.Take 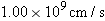 and and 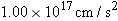 . (Why don’t you need to know the width of the boxcar?) . (Why don’t you need to know the width of the boxcar?) |
| 118. |
You are to throw a ball with a speed of 12.0 m/s at a target that is height
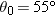 above the level at which you release the ball (Fig. 4-60). You want the ball’s velocity to be horizontal at the instant it reaches the target. (a) At what angle above the level at which you release the ball (Fig. 4-60). You want the ball’s velocity to be horizontal at the instant it reaches the target. (a) At what angle 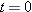 above the horizontal must you throw the ball? (b) What is the horizontal distance from the release point to the target? (c) What is the speed of the ball just as it reaches the target? above the horizontal must you throw the ball? (b) What is the horizontal distance from the release point to the target? (c) What is the speed of the ball just as it reaches the target?
|
| 119. |
| 120. |
| 121. |
Oasis A is 90 km due west of oasis B. A desert camel leaves A and takes 50 h to walk 75 km at 37° north of due east. Next it takes 35 h to walk 65 km due south. Then it rests for 5.0 h. What are the (a) magnitude and (b) direction of the camel’s displacement relative to A at the resting point? From the time the camel leaves A until the end of the rest period, what are the (c) magnitude and (d) direction of its average velocity and (e) its average speed? The camel’s last drink was at A; it must be at B no more than 120 h later for its next drink. If it is to reach B just in time, what must be the (f) magnitude and (g) direction of its average velocity after the rest period?
|
| |||||||||||||
| 122. |
A graphing surprise. At time
 , a burrito is launched from level ground, with an initial speed of 16.0 m/s and launch angle , a burrito is launched from level ground, with an initial speed of 16.0 m/s and launch angle  . Imagine a position vector . Imagine a position vector 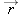 continuously directed from the launching point to the burrito during the flight. Graph the magnitude r of the position vector for (a) continuously directed from the launching point to the burrito during the flight. Graph the magnitude r of the position vector for (a) 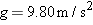 and (b) and (b) 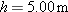 . For . For 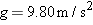 , (c) when does r reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For , (c) when does r reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For 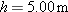 , (g) when does r reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point? , (g) when does r reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point? |
| 123. |
In Sample Problem 4-7b, a ball is shot through a horizontal distance of 686 m by a cannon located at sea level and angled at 45° from the horizontal. How much greater would the horizontal distance have been had the cannon been 30 m higher?
|
| 124. |
(a) If an electron is projected horizontally with a speed of
 , how far will it fall in traversing 1.0 m of horizontal distance? (b) Does the answer increase or decrease if the initial speed is increased? , how far will it fall in traversing 1.0 m of horizontal distance? (b) Does the answer increase or decrease if the initial speed is increased? |
| 125. |
The magnitude of the velocity of a projectile when it is at its maximum height above ground level is 10 m/s. (a) What is the magnitude of the velocity of the projectile 1.0 s before it achieves its maximum height? (b) What is the magnitude of the velocity of the projectile 1.0 s after it achieves its maximum height? If we take
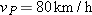 and and 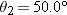 to be at the point of maximum height and positive x to be in the direction of the velocity there, what are the (c) x coordinate and (d) y coordinate of the projectile 1.0 s before it reaches its maximum height and the (e) x coordinate and (f) y coordinate 1.0 s after it reaches its maximum height? to be at the point of maximum height and positive x to be in the direction of the velocity there, what are the (c) x coordinate and (d) y coordinate of the projectile 1.0 s before it reaches its maximum height and the (e) x coordinate and (f) y coordinate 1.0 s after it reaches its maximum height? |
| 126. |
A frightened rabbit moving at 6.0 m/s due east runs onto a large area of level ice of negligible friction. As the rabbit slides across the ice, the force of the wind causes it to have a constant acceleration of
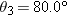 , due north. Choose a coordinate system with the origin at the rabbit’s initial position on the ice and the positive x axis directed toward the east. In unitvector notation, what are the rabbit’s (a) velocity and (b) position when it has slid for 3.0 s? , due north. Choose a coordinate system with the origin at the rabbit’s initial position on the ice and the positive x axis directed toward the east. In unitvector notation, what are the rabbit’s (a) velocity and (b) position when it has slid for 3.0 s? |
| 127. |
The pilot of an aircraft flies due east relative to the ground in a wind blowing 20 km/h toward the south. If the speed of the aircraft in the absence of wind is 70 km/h, what is the speed of the aircraft relative to the ground?
|
| 128. |
The pitcher in a slow-pitch softball game releases the ball at a point 3.0 ft above ground level. A stroboscopic plot of the position of the ball is shown in Fig. 4-63, where the readings are 0.25 s apart and the ball is released at
 . (a) What is the initial speed of the ball? (b) What is the speed of the ball at the instant it reaches its maximum height above ground level? (c) What is that maximum height? . (a) What is the initial speed of the ball? (b) What is the speed of the ball at the instant it reaches its maximum height above ground level? (c) What is that maximum height?
|
| 129. |
The New Hampshire State Police use aircraft to enforce highway speed limits. Suppose that one of the airplanes has a speed of 135 mi/h in still air. It is flying straight north so that it is at all times directly above a north–south highway. A ground observer tells the pilot by radio that a 70.0 mi/h wind is blowing but neglects to give the wind direction. The pilot observes that in spite of the wind the plane can travel 135 mi along the highway in 1.00 h. In other words, the ground speed is the same as if there were no wind. (a) From what direction is the wind blowing? (b) What is the heading of the plane; that is, in what direction does it point?
|
| 130. |
The position
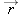 of a particle moving in the xy plane is given by of a particle moving in the xy plane is given by 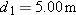 , where , where 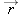 is in meters and t is in seconds. (a) Calculate the x and y components of the particle’s position at is in meters and t is in seconds. (a) Calculate the x and y components of the particle’s position at 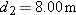 , and 4.0 s and sketch the particle’s path in the xy plane for the interval , and 4.0 s and sketch the particle’s path in the xy plane for the interval  . (b) Calculate the components of the particle’s velocity at . (b) Calculate the components of the particle’s velocity at  , 2.0, and 3.0 s. Show that the velocity is tangent to the path of the particle and in the direction the particle is moving at each time by drawing the velocity vectors on the plot of the particle’s path in part (a). (c) Calculate the components of the particle’s acceleration at , 2.0, and 3.0 s. Show that the velocity is tangent to the path of the particle and in the direction the particle is moving at each time by drawing the velocity vectors on the plot of the particle’s path in part (a). (c) Calculate the components of the particle’s acceleration at  , 2.0, and 3.0 s. , 2.0, and 3.0 s. |
| 131. |
A golfer tees off from the top of a rise, giving the golf ball an initial velocity of 43 m/s at an angle of 30° above the horizontal. The ball strikes the fairway a horizontal distance of 180 m from the tee. Assume the fairway is level. (a) How high is the rise above the fairway? (b) What is the speed of the ball as it strikes the fairway?
|
| 132. |
A track meet is held on a planet in a distant solar system. A shot-putter releases a shot at a point 2.0 m above ground level. A stroboscopic plot of the position of the shot is shown in Fig. 4-64, where the readings are 0.50 s apart and the shot is released at time
 . (a) What is the initial velocity of the shot in unit-vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground? . (a) What is the initial velocity of the shot in unit-vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground?
|
| Copyright © 2008 John Wiley & Sons, Inc. All rights reserved. |