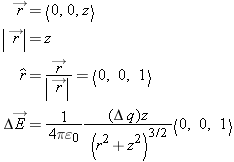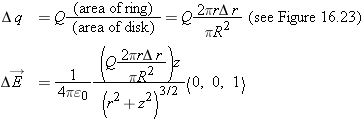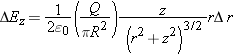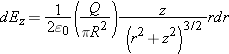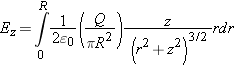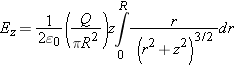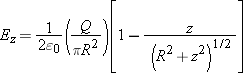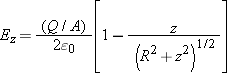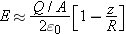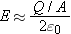One reason that a uniformly charged disk is important is that two oppositely charged metal disks can form a “capacitor,” a device that is important in electric circuits. Before discussing metal disks, we will consider a glass disk that has been rubbed with silk in such a way as to deposit a uniform density of positive charge all over the surface.

The electric field of a uniformly charged disk of course varies in both magnitude and direction at observation locations near the disk, as illustrated in Figure 16.21, which shows the computed pattern of electric field at many locations near a uniformly charged disk (done by numerical integration, with the surface of the disk divided into small areas). Note, however, that near the center of the disk the field is quite uniform for a given distance from the disk. Even near the edge of the disk the magnitude of the electric field isn't very different, though the direction is no longer nearly perpendicular to the disk.

Figure 16.21    A uniformly charged disk viewed edge-on. The electric field is shown at locations across the diameter of the disk. Note the uniformity of the field near the central region of the disk for a given distance from the disk.

Again, we'll pick an easy location for an analytical solution—the field at any location along the axis of the disk, which is a line going through the center and perpendicular to the disk, as shown in Figure 16.22. This is a more useful choice than one might expect, since the field turns out to be nearly uniform in regions far from the edge of the disk as can be seen in Figure 16.21; our result will be applicable to a variety of situations.

Figure 16.22    A ring of width Δr makes a contribution ΔE to the total electric field.

We consider a disk of radius R, with a total charge Q uniformly distributed over the front surface of the disk.

Use thin concentric rings as pieces, as shown in Figure 16.22, since we already know the electric field of a uniform ring. Approximate each ring as having some average radius r.

Origin: Center of ring.

Location of piece: Given by radius r of ring.

Integration variable: r

Note that both Δq and r will be different for each piece.

Δq in terms of variables:

Figure 16.23    A ring of radius r and thickness Δr cut and rolled out straight.

Components to calculate: Only ΔE_z is nonzero. or, for infinitesimally thin rings:

Many of these quantities have the same values for different values of r, and these can be taken out of the integral as common factors: This particular integral can be done by a change of variables, letting u = (r² +z²). You can work it out yourself, look up the result in a table of integrals, or use a symbolic math package or calculator to evaluate it. The result is: for a uniformly charged disk of charge Q and radius R, at locations along the axis of the disk. This is often written in terms of the area A of the disk (A = π R²):

Direction: Away from the disk if Q is positive, as expected.

Special location: 0 << z << R (very close to the disk, but not touching it. See Figure 16.25.)

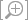
Figure 16.25    Magnitude of electric field along the axis of a disk, for z < 0.1R.

If z/R is extremely small, [1 − z/R] reduces to 1, and Interestingly, this field is nearly independent of distance! This result is approximately true near any large uniformly charged plate, not just a circular one.

	Electric Field of a Uniformly Charged Disk
	at a location along the axis, a distance z from the disk (Figure 16.24). The direction is perpendicular to the surface of the disk. Q is the total charge on the disk, A is the area of the surface of the disk, and R is the radius of the disk.    Figure 16.24    Electric field of a uniformly charged disk, at a location on the axis.

	Approximate Electric Field of a Uniformly Charged Disk
	or at a location a perpendicular distance z << R from the disk, as long as the observation location is not too near the edge of the disk (Figure 16.25). The direction is perpendicular to the surface of the disk. Q is the total charge on the disk, A is the area of the surface of the disk, and R is the radius of the disk.

Although we proved this result only for observation locations a perpendicular distance z << R from the center of the disk, the result is actually a good approximation as long as you're not too near the edge of the disk, as can be seen in Figure 16.21, which is the result of an accurate numerical integration.