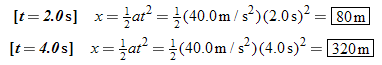|
A top-fuel dragster starts from rest and has a constant acceleration of 40.0 m/s2. What are the (a) final velocities and (b) displacements of the dragster at the end of 2.0 s and at the end of twice this time, or 4.0 s?
Concept Questions and Answers At a time t the dragster has a certain velocity. When the time doubles to 2t, does the velocity also double?
 | Answer
Because the dragster has an acceleration of 40.0 m/s2, its velocity changes by 40.0 m/s during each second of travel. Therefore, since the dragster starts from rest, the velocity is 40.0 m/s at the end of the 1st second, 2 × × 40.0 m/s at the end of the 2nd second, 3 40.0 m/s at the end of the 2nd second, 3 × × 40.0 m/s at the end of the 3rd second, and so on. Thus, when the time doubles, the velocity also doubles. 40.0 m/s at the end of the 3rd second, and so on. Thus, when the time doubles, the velocity also doubles.
|
When the time doubles to 2t, does the displacement of the dragster also double?
 | Answer
The displacement of the dragster is equal to its average velocity multiplied by the elapsed time. The average velocity 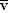 is just one-half the sum of the initial and final velocities, or is just one-half the sum of the initial and final velocities, or 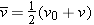 . Since the initial velocity is zero, v0 . Since the initial velocity is zero, v0 = = 0 m/s and the average velocity is just one-half the final velocity, or 0 m/s and the average velocity is just one-half the final velocity, or 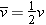 . However, as we have seen, the final velocity is proportional to the elapsed time, since when the time doubles, the final velocity also doubles. Therefore, the displacement, being the product of the average velocity and the time, is proportional to the time squared, or t2. Consequently, as the time doubles, the displacement does not double, but increases by a factor of four. . However, as we have seen, the final velocity is proportional to the elapsed time, since when the time doubles, the final velocity also doubles. Therefore, the displacement, being the product of the average velocity and the time, is proportional to the time squared, or t2. Consequently, as the time doubles, the displacement does not double, but increases by a factor of four.
|
Solution
| (a) |
According to Equation 2.4, the final velocity v, the initial velocity v0, the acceleration a, and the elapsed time t are related by v = = v0 v0 + + at. The final velocities at the two times are
We see that the velocity doubles when the time doubles, as expected. at. The final velocities at the two times are
We see that the velocity doubles when the time doubles, as expected.
| | (b) |
The displacement x of the dragster is equal to its average velocity multiplied by the time, so
where we have used the fact that v0 = = 0 m/s. According to Equation 2.4, the final velocity is related to the acceleration by v 0 m/s. According to Equation 2.4, the final velocity is related to the acceleration by v = = v0 v0 + + at, or v at, or v = = at, since v0 at, since v0 = = 0 m/s. Therefore, the displacement can be written as 0 m/s. Therefore, the displacement can be written as 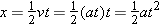 . The displacements at the two times are then
As predicted, the displacement at t . The displacements at the two times are then
As predicted, the displacement at t = = 4.0 s is four times the displacement at t 4.0 s is four times the displacement at t = = 2.0 s. 2.0 s.
|
|

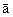 is the change in the velocity divided by the elapsed time:
is the change in the velocity divided by the elapsed time:
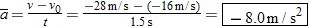
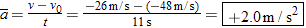
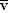 is just one-half the sum of the initial and final velocities, or
is just one-half the sum of the initial and final velocities, or 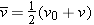 . Since the initial velocity is zero,
. Since the initial velocity is zero, 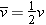 . However, as we have seen, the final velocity is proportional to the elapsed time, since when the time doubles, the final velocity also doubles. Therefore, the displacement, being the product of the average velocity and the time, is proportional to the time squared, or
. However, as we have seen, the final velocity is proportional to the elapsed time, since when the time doubles, the final velocity also doubles. Therefore, the displacement, being the product of the average velocity and the time, is proportional to the time squared, or 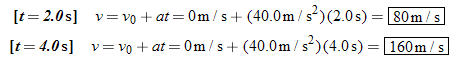
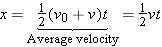
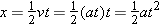 . The displacements at the two times are then
. The displacements at the two times are then