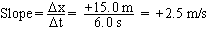Graphical Analysis of Velocity and Acceleration

2.7. Graphical Analysis of Velocity and Acceleration

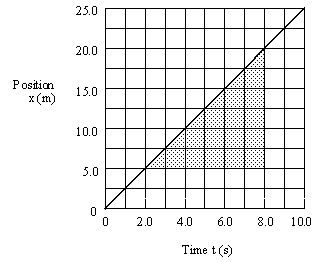
Consider an object moving in a straight line at a constant speed. The position, x, is plotted as a function of time, t, in the following graph.

We can see from the graph that the position is increasing linearly with time, i.e., the graph is a straight line. Between the times 2.0 and 8.0 s note that the object travels from 5.0 to 20.0 m. The change in time is Dt = 6.0 s, while the change in position is Dx = +15.0 m. The ratio of Dx/Dt is called the slope of the straight line. That is

Note that the slope has units of velocity (m/s). In fact, the slope of the position vs. time graph does represent the average velocity of the moving object, as evidenced by the fact that the above equation is identical to equation (2.2). In the real world, however, the situation may not be quite as simple. Consider the following example.

Example 7 Determining the slope of a position vs. time graph

Consider the following position vs. time graph and determine the velocity over each segment.

Segment A: v = Dx/Dt = (+30.0 m)/(40.0 s) = +0.750 m/s.

Segment B: v = Dx/Dt = (0 m)/(40.0 s) = 0 m/s.

Segment C: v = Dx/Dt = (-20.0 m)/(80.0 s) = -0.250 m/s.

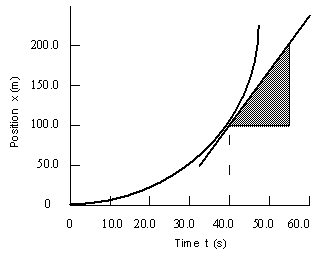
In segment A the object is traveling with a positive velocity of 0.75 m/s. Over segment B the object does not change position, so its velocity is zero. Over segment C the slope of the graph is negative and hence the velocity is negative, i.e., the object is now moving in the negative direction. Example 8 Accelerated motion, slope of a tangent line

Using the position vs. time graph shown at the right, we can determine the velocity of the object at say, t = 40 s. We see that the velocity is changing with time. The velocity at any instant of time can be determined by measuring the slope of the tangent to the curve at that point.

This will then provide us with a value of the instantaneous velocity at the point in question.

The slope at t = 40.0 s can be determined by referring to the shaded triangle. The slope is

v = slope = Dx/Dt = (200.0 m-100.0 m)/(55.0 s-40.0 s) = (+100.0 m)/(15.0 s) = +6.67 m/s.

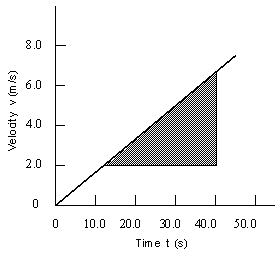
If we were to plot a graph of velocity vs. time for the data in the drawing for Example 8 we would obtain the graph shown at the right. Its slope is:

Slope = Dv/Dt = (6.7 m/s - 2.0 m/s)/(40.0 s - 12.0 s) = (+4.7 m/s)/(28.0 s) = +0.17 m/s².

Notice that the slope of the velocity vs. time graph represents the acceleration of the object over this time interval.