PRACTICE PROBLEMS
A car travels 10.0 km due north, then 8.00 km due east, the total trip taking 30.0 minutes. Find (a) the displacement of the car, (b) the average speed (in m/s), and (c) the average velocity (in m/s).
| a. |
The total displacement is the vector sum of the individual displacements. Since these displacements are perpendicular, the vector sum is given by the Pythagorean theorem.
| x2 = (10.0 km)2 + (8.00 km)2
|  |
| x = 12.8 km. |  |
The angle is found using
| tan q = (10.0 km/8.00 km) |  |
|
q = 51.3° N of E.
|  |
|
| b. |
Avg. Speed = Distance/Time = (18.0 km/30.0 min)(1000 m/1 km)(1 min/60 s) = 10.0 m/s.
|
| c. |
Avg. Velocity = Displacement/Time = (12.8 km/30.0 min)(1000 m/1 km)(1 min/60 s) = 7.11 m/s.
|
A bicycle accelerates to a velocity of 25.0 mi/h in 5.00 s. The average acceleration over this time interval is 4.00 ft/s2. What was the initial velocity of the bike?
The average acceleration is given by equation (2.4),
| a = Dv/Dt = (v - v0)/Dt |  |
or
| v0 = v - at |  |
where
| v = (25.0 mi/h)(5280 ft/1 mi)(1 h/3600 s) = 36.7 ft/s. |  |
Then
| v0 = 36.7 ft/s - (4.00 ft/s2)(5.00 s) = 16.7 ft/s.
|  |
A train accelerates from rest to a speed of 25.0 m/s in 10.0 s. Assuming the acceleration to be constant over this interval find (a) the magnitude of the acceleration, and (b) the distance traveled during this interval.
| a. |
Using equation (2.4) we have
| a = (v - v0)/Dt = (+25.0 m/s)/(10.0 s) = +2.50 m/s2.
|  |
|
| b. |
Using equation (2.7) we have
| x = (1/2)(v + v0)t = (1/2)(25.0 m/s + 0)(10.0 s) = 125 m.
|  |
|
A drag racer, starting from rest, travels a quarter mile in 6.0 s. What is the racer's speed (in mi/h) at the end of the race?
Using v0 = 0, x = (0.250 mi)(5280 ft/mi) = 1320 ft, t = 6.0 s and equation (2.7) we solve for v to get
| v = 2x/t = 2(1320 ft)/(6.0 s) = (440 ft/s)(1 mi/5280 ft)(3600 s/1 h) = 3.0 × 102 mi/h.
|  |
Suppose a car traveling at 12.0 m/s sees a traffic light turn red. After 0.510 s have elapsed, the driver applies the brakes, and the car decelerates at 6.20 m/s2. What is the stopping distance of the car, as measured from the point where the driver first notices the red light?
The motion should be divided into two segments; segment 1 is constant velocity and segment 2 is deceleration.
| x1 = v0t = (12.0 m/s)(0.510 s) = 6.12 m; |  |
| x2 = (v2 - v0
2)/2a = -(12.0 m/s)2/[2(-6.20 m/s2)] = 11.6 m. |  |
The stopping distance is therefore
| x = x1 + x2 = 6.12 m + 11.6 m = 17.7 m.
|  |
A car starts from rest heading due east. It first accelerates at 3.0 m/s2
for 5.0 s and then continues without further acceleration for 20.0 s. It then brakes for 8.0 s in coming to rest. (a) What is the car's velocity after the first 5.0 seconds? (b) What is the car's acceleration over the last 8.0 s interval? (c) What is the total displacement?
| a. |
a = 3.0 m/s2, t = 5.0 s, v0 = 0. Equation (2.4) gives
| v = v0 + at = (3.0 m/s2)(5.0 s) = 15 m/s East.
|  |
|
| b. |
v0 = 15 m/s, v = 0, t = 8.0 s. Equation (2.4) gives
| a = (v - v0)/t = (-15 m/s)/(8.0 s) = 1.9 m/s2 West.
|  |
|
| c. |
The distance is then
| x = x1 + x2 + x3 = (1/2)a1t1
2 + v2t2 + + v2t3 + (1/2)a3t3
2 = 4.0 × 102 m.
|  |
|
A ball is thrown upward with an initial velocity of 20.0 m/s. What maximum height does the ball reach?
v0 = 20.0 m/s, v = 0, a = -9.80 m/s2. Equation (2.9) is
| v2 = v0
2 + 2ax |  |
Solving for x we obtain
| x = -v0
2/2a = -(20.0 m/s)2/[2(-9.80 m/s2)] = 20.4 m.
|  |
A stone is thrown vertically downward from a 2.00× 102 m high cliff at an initial velocity of 5.00 m/s. (a) How long does it take for the stone to reach the base of the cliff? (b) What is the stone's final velocity?
| a. |
v0 = 5.00 m/s, a = 9.80 m/s2, x = 2.00× 102 m. Equation (2.8): x = v0t + (1/2)at2.
Substituting yields the quadratic equation
| 4.90 t2 + 5.00 t - 2.00× 102 = 0 |  |
which has a solution
| t = 5.90 s.
|  |
|
| b. |
Since
| v2 = v0
2 + 2ax = (5.00 m/s)2 + 2(9.80 m/s2)(2.00× 102 m) |  |
then
| v = 62.8 m/s.
|  |
|
A sports car, picking up speed, passes between two markers in a time of 4.1 s. The markers are separated by 120 m. All the while, the car accelerates at 1.8 m/s2. What is its speed at the second marker?
a = 1.8 m/s2, x = 120 m, t = 4.1 s. Equation (2.8),
| x = v0t + (1/2)at2
|  |
yields
| v0 = [x - (1/2)at2]/t = 25.6 m/s. |  |
Equation (2.4), gives
| v = v0 + at = 25.6 m/s + (1.8 m/s2)(4.1 s) = 33 m/s.
|  |
A heavy ball is dropped into a lake from a height of 30.0 m above the water. It hits the water with a certain velocity and continues to sink to the bottom of the lake at this same constant velocity. It reaches the bottom of the lake 10.0 s after it was dropped. How deep is the lake?
Find the velocity with which the ball hits the water and the time it takes to do so. Since v0 = 0 we have
| x = (1/2)at2
|  |
which gives
Now
| v = at = (9.80 m/s2)(2.47 s) = 24.2 m/s. |  |
The time it takes to sink is
| t' = 10.0 s - 2.47 s = 7.5 s. |  |
The depth of the lake is therefore found from
| Depth = vt' = (24.2 m/s)(7.5 s) = 180 m.
|  |
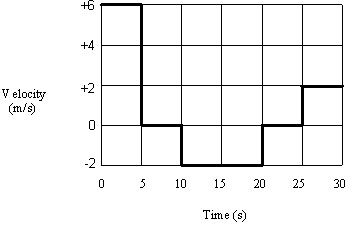
Using the position-time graph shown below, draw the corresponding velocity-time graph.
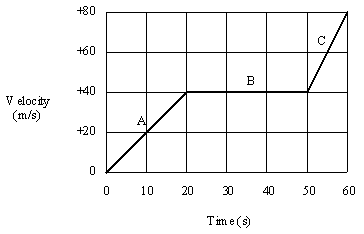
A snowmobile moves according to the velocity-time graph shown below. What is the snowmobile's average acceleration during each of the segments labeled A, B, and C?
During segment:
 | A: |  | a = (40 m/s)/(20 s) = 2 m/s2
. |  |
 | B: |  | a = (0 m/s)/(30 s) = 0 m/s2
. |  |
 | C: |  | a = (40 m/s)/(10 s) = 4 m/s2
. |  |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |