Equations of Kinematics in Two Dimensions

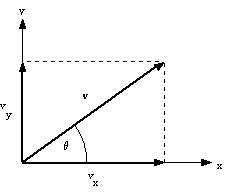
3.2. Equations of Kinematics in Two Dimensions

In Chapter 2 we emphasized that displacement, velocity, and acceleration were vector quantities. In one-dimensional motion the direction of these vectors was simply denoted by a positive or negative sign. In the more complex realm of two dimensions we must be careful to treat both the x and y motion independently, with the understanding that they will add together as vectors.

In treating two-dimensional motion we must be careful to view the x and y components of the motion as separate but related quantities. We will see that the x part of the motion occurs exactly as it would if the y part did not occur at all. Similarly, the y part of the motion occurs exactly as it would if the x part of the motion did not exist. Therefore, two sets of kinematic equations are needed to describe the full two dimensional motion.

Example 1 Components of the velocity vector

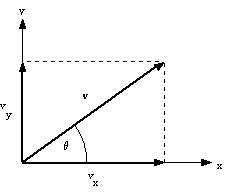A ball is traveling at a constant velocity of 20.0 m/s at an angle of 30.0 degrees with respect to the x axis. How far does the ball travel in the x and y directions in 1 minute? See the diagram shown below.

First find the x and y components of the velocity.

v_x = v cos q = (20.0 m/s)cos 30.0° = 17.3 m/s.

v_y = v sin q = (20.0 m/s)sin 30.0° = 10.0 m/s.

Since there is no acceleration, the x and y displacements are given by equations (3.5a) and (3.5b) with v_0x = v_x and v_0y = v_y. We therefore have,

x = v_x t = (17.3 m/s) (60 s) = 1040 m.

y = v_y t = (10.0 m/s) (60 s) = 600 m.