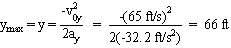3.3.
Projectile Motion
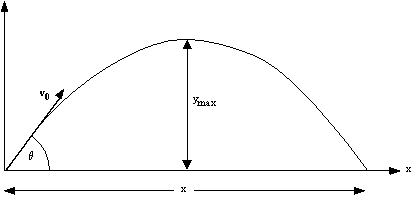
When we throw a ball, or fire a bullet from a gun, the motion is one in which only the vertical component of the velocity changes with time. The horizontal velocity component remains constant (assuming that air resistance is negligible). We refer to this type of motion as projectile motion. The equations describing the trajectory of such a projectile are equations (3.3) through (3.6). Consider the following example.
Example 2
A football is kicked with an initial velocity of 82 ft/s at an angle of 53° with respect to the horizontal. How high does the football go and how far down the field does it land?
The x and y motions can be treated separately. Begin by looking at the motion in the y direction. We have
| v0y = v0 sin q = (82 ft/s) sin 53° = 65 ft/s; ay = -32.2 ft/s2; vy = 0. |  |
Notice we have chosen the final velocity to be zero. In effect, we are looking at the first half of the motion in the y direction, i.e., the portion of the motion in which the ball is rising. When the ball reaches its maximum height, vy = 0 and y = ymax. Using equation (3.6b) we can solve for this maximum height y,
To find the distance the football travels in the x direction, we need to know the time of flight for the ball. We can find the time it takes for the ball to rise using equation (3.3b), i.e.,
| t = -v0y/ ay = -(65 ft/s)/(-32.2 ft/s2) = 2.0 s. |  |
The total time of flight is twice this value, or 4.0 seconds. Now we can find the x distance using equation (3.5a) and noting that ax = 0 and v0x = v0 cos q = (82 ft/s) cos 53° = 49 ft/s. We have
| x = v0xt = (49 ft/s) (4.0 s) = 2.0 × 102 ft. |  |
So the ball rose 66 ft in the air, stayed up in the air 4.0 s (hang time), and traveled 2.0× 102 ft.
Example 3
A jet fighter is traveling horizontally with a speed of 111 m/s at an altitude of 3.00× 102 m, when the pilot accidentally releases an outboard fuel tank. (a) How much time elapses before the tank hits the ground? (b) What is the speed of the tank just before it hits the ground? (c) What is the horizontal distance traveled by the tank?
| (a) | The y direction data is: y = - 3.00 × 102 m, v0y = 0, ay = - 9.80 m/s2. Using equation (3.5b) and solving for t,
|
| (b) | The y component of the velocity as it strikes the ground can be found using equation (3.3b),
The speed as it hits the ground can be obtained by calculating the vector sum of the x and y components. The x component of the velocity is constant at 111 m/s. Therefore,
|
| (c) | The horizontal distance can be obtained using equation (3.5a) with ax = 0 and v0x = 111 m/s,
| x = v0x t = (111 m/s) (7.82 s) = 868 m. |  |
|
Note that the initial velocity, v0x, plays no role in determining the time required for the fuel tank to hit the ground. Even if the jet were moving faster, the tank would still take 7.82 s to reach the ground. However, the speed on impact and the horizontal distance would be affected by v0x.
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |