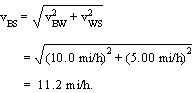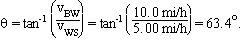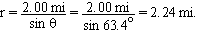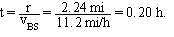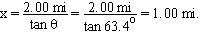Relative Velocity

3.4. Relative Velocity

The velocity measured for a particular object depends on the observer who is making the measurement. For example, suppose a ground based observer is measuring the velocity of two cars, each moving in the same direction. Car A is moving at 45 km/h relative to the ground, while car B is moving at 55 km/h relative to the ground. The observer in car A, however, measures the velocity of car B as 10 km/h relative to himself. Car B measures A's velocity as -10 km/h in his reference frame. So each observer obtains different values for the velocities because each is making measurements from different points of reference.

Example 4 Relative velocity in one dimension

A passenger in a moving train is walking towards the dining car in the front of the train. The train is moving at a speed of 21 ft/s and the passenger is walking at 4 ft/s relative to the train. How far will the passenger move in 10.0 seconds relative to (a) the train, and (b) a ground based observer.

Use the following symbols to represent the different relative velocities:

v_TG = velocity of the train relative to the ground.

v_PT = velocity of the passenger relative to the train.

v_PG= velocity of the passenger relative to the ground.

We can see that the three velocities are related in the following manner:

v_PG = v_PT + v_TG = 4 ft/s + 21 ft/s = 25 ft/s.

The distances measured in each case are therefore,

(a)

s_PT= v_PTt = (4 ft/s) (10.0 s) = 40 ft.

(b)

s_PG = v_PGt = (25 ft/s) (10.0 s) = 250 ft.

When dealing with relative velocities in two dimensions it is important to emphasize the vector nature of the velocities. For example, if a boat is sailing across a stream, and the stream is flowing, both the boat's and the stream's velocity must be considered. Similarly, the velocity of an airplane in flight is effected by the velocity of the wind. The following example illustrates this effect. Example 5 Relative velocity in two dimensions

A boat whose speed is 10.0 mi/h in still water travels across a river that is 2.00 miles wide. The river current is 5.00 mi/h directed parallel to the river bank. How long does it take for the boat to cross the river and how far downstream will the boat arrive?

First find the velocity of the boat relative to the shore. From the diagram we can see that

v_BS = v_BW + v_WS

Since the vectors v_BW and v_WS are perpendicular to each other, the magnitude and direction of v_BS can be found from the Pythagorean theorem.

To find the amount of time and downstream distance we need to know the angle q shown in Figure A. We have

In order to find the time taken for the trip we need the total distance traveled. We see that this distance is

Note that the angle q that v_BS makes with v_WS (in Figure A) is the same angle q that r makes with x (in Figure B). Therefore, the time taken for the boat to cross the river can be obtained using

The distance the boat lands downstream can be found from