PRACTICE PROBLEMS
A pitcher throws a baseball at a speed of 90.0 mi/h towards home plate, which is located 60.0 ft away. How far has the ball dropped when it reaches the plate? Assume the ball leaves the pitcher's hand traveling horizontally.
The horizontal speed is
| vx = (90.0 mi/h)(1h/3600 s)(5280 ft/1 mi) = 132 ft/s. |  |
The time to travel 60.0 ft is
| t = x/vx = (60.0 ft)/(132 ft/s) = 0.455 s. |  |
| y = v0yt + (1/2)ayt2 = 0 + (1/2)(32.2 ft/s2)(0.455 s)2 = 3.33 ft.
|  |
An arrow is shot at an initial velocity of 25.0 m/s at an angle of 30.0 degrees with respect to the horizontal. (a) What is the maximum height reached by the arrow? (b) How far does the arrow travel in the horizontal direction in returning to the same level from which it was shot?
| a. |
The initial velocity is
| v0y = v0 sin 30.0° = (25.0 m/s)(0.500) = 12.5 m/s; |  |
Use equation (3.6b) and solve for y
| y = -v0
2/2ay = - (12.5 m/s)2/[2(-9.80 m/s2)] = 7.97 m.
|  |
|
| b. |
Find the time from vy = v0y + ayt
| t = -v0y/ay = - (12.5 m/s)/(-9.80 m/s2) = 1.28 s. |  |
Finally, we have
| x = v0xt = v0 cos 30.0° t = (25.0 m/s) cos 30.0° (2.56 s) = 55.4 m.
|  |
|
A plane is traveling at a velocity of 2.0 × 102 m/s at an angle of 45 degrees below the horizontal. It releases a bomb at an altitude of 1.0 × 103 m, which strikes a target on the ground. (a) How far was the plane from the target when the bomb was released? (b) How long did it take the bomb to strike the target after being released? (c) What was the bomb's speed at the moment of impact?
Using equation (3.6b) we have
| vy
2 = v0y
2 + 2ayy = [(2.0 × 102 m/s) sin 45°]2 + 2(-9.80 m/s2)(-1.0 × 103m), |  |
which yields vy = 2.0 × 102 m/s. Now, vx = v0 cos 45° = 141 m/s. The time can be found from equation (3.3b),
| t = (vy - v0y)/ ay = (2.0 × 102 m/s - 1.4 × 102 m/s)/(9.80 m/s2) = 6.1 s. |  |
| a. |
x = v0xt = (141 m/s)(6.1 s) = 860 m, y = 1.0 × 103 m,
| s2 = x2 + y2 = (860 m)2 + (1.0 × 103 m)2, so that s = 1300 m.
|  |
|
| b. |
We have already seen that t = 6.1 s.
|
| c. |
Finally,
| v2 = vx
2 + vy
2 = (141 m/s)2 + (2.0 × 102 m/s)2 so v = 240 m/s.
|  |
|
A diver springs upward from a three-meter board. At the instant she contacts the water her speed is 8.90 m/s and her body makes an angle of 75.0° with respect to the surface of the water. (a) Determine her initial velocity, both magnitude and direction. (b) How much time does she spend in the air?
| a. |
At a height of 3.00 m above the water find v0. We know
| vy = v sin 75.0° = (8.90 m/s)sin 75.0° = 8.60 m/s. |  |
From equation (3.6b) we have
v0y
2 = vy
2 - 2ayy = (8.60 m/s)2 - 2(9.80 m/s2)(3.00 m)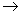 v0y = 3.89 m/s. v0y = 3.89 m/s. |  |
Also,
v0x = vx = v cos 75.0° = (8.90 m/s) cos 75.0° = 2.30 m/s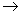 v0
2 = v0x
2 + v0y
2 so that v0
2 = v0x
2 + v0y
2 so that |  |
| v0 = 4.52 m/s.
|  |
The direction is obtained from
|
q = tan-1(v0y/v0x) = tan-1[(3.89 m/s)/(2.30 m/s)] = 59.4°.
|  |
|
| b. |
The time to go up is tup = -v0y/ ay = 0.397 s; the time down is tdown = vy/ ay = 0.878 s. So total time is
| t = tup + tdown = 0.40 s + 0.88 s = 1.28 s.
|  |
|
A ball rolls off the top of a stairway with a horizontal velocity of 2.0 m/s. The steps are each 20.0 cm high and 20.0 cm wide. Which step will the ball hit first?
In order to determine which step the ball lands on, the ball must fall at least a distance equal to its horizontal displacement. For example, at x = 0.2 m,
| t = x/vx = (0.2 m)/(2.0 m/s) = 0.1 s, |  |
| y = (1/2)ayt2 = 0.05 m. |  |
So the ball goes past the first step. At x' = 0.8 m (4th step), t' = 0.4 s and y' = 0.78 m, so it goes past the 4th step. However, at x" = 1.0 m (5th step), t" = 0.5 s, y" = 1.23 m. So the ball lands on the fifth step.
When a cannon is aimed at an angle of 45° above the horizontal, a cannon ball lands 1.0 × 102 m down range. What was the muzzle velocity of the cannon ball?
The time taken to travel half the distance in the x direction, using equation (3.5a), is
| t = x/(v0 cos 45°) = (50.0 m)/(v0 cos 45°). |  |
The time it takes for the ball to reach its maximum height is the also this value of t, and using equation (3.3b) with vy = 0,
| t = v0y/ ay = v0sin 45°/(9.8 m/s2). |  |
Equating the two expressions for the time, and noting that cos 45° = sin 45° yields,
| (v0 cos 45°)2 = (50.0 m)(9.8 m/s2). |  |
Thus,
| v0
2 = (50.0 m)(9.8 m/s2)/(cos2 45°) |  |
| v0 = 31 m/s.
|  |
The compass of an aircraft indicates it is headed due north, and its airspeed indicator shows that it is moving through the air at 120 mi/h. If a wind of 50.0 mi/h blowing from west to east suddenly arises, what is the velocity of the aircraft relative to the earth?
A vector diagram shows that
| v2 = vP
2 + vW
2 = (120 mi/h)2 + (50.0 mi/h)2
|  |
| v = 130 mi/h.
|  |
The direction is
|
q = tan-1 (vP/vW) = tan-1 [(120 mi/h)/(50.0 mi/h)] = 67° North of East.
|  |
An airplane pilot wishes to fly due south. A wind of 25 km/h is blowing toward the west. If the flying speed of the plane is 300.0 km/h (its speed in still air), in what direction should the pilot head?
Since the final direction of motion and the direction of the wind are perpendicular, we can find the angle between the plane and wind, i.e.,
|
q = cos-1 (vW/vP) = cos-1 [(25 km/h)/(300.0 km/h)] = 85° S of E.
|  |
Two trains approach a railroad station, one from the north at 30.0 m/s, the other from the east at 40.0 m/s. Find the velocities of (a) the railroad station and (b) the south-bound train; relative to the west-bound train.
| a. |
We can write
v
RW = v
RG + v
GW
where R 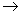 railroad station, W railroad station, W 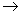 west bound train, G west bound train, G  ground.
So ground.
So
| vRW = 0 + 40 m/s = 40 m/s East.
|  |
|
| b. |
We have
vSW = vSG + vGW
. Since
vSG
and
vGW
are perpendicular, we can write vSW
2 = vSG
2 + vGW
2. So,
| vSW
2 = (30.0 m/s)2 + (40.0 m/s)2
|  |
| vSW = 50.0 m/s.
|  |
Also,
|
q = tan-1 (vSG/vGW) = 36.9
°
S of E.
|  |
|
A boat can travel at a speed of 20.0 km/h relative to the water. The boat sails across a river (perpendicular to the river bank) and reaches a point 5.00 km directly across from its launch point. The water is flowing at a speed of 8.00 km/h parallel to the river bank. (a) At what angle must the boat steer to reach its destination? (b) How much time is required for the boat to make the trip?
| a. |
A vector diagram shows that the angle at which the boat must steer is
q = cos-1 (vS/vB), where the velocity vS
is that of the stream and vB
is that of the boat. So,
|
q = cos-1 [(8.00 km/h)/(20.0 km/h)] = 66.4°.
|  |
|
| b. |
The velocity across the river is
| v2 = vB
2 - vS
2 = (20.0 km/h)2 - (8.00 km/h)2
|  |
| v = 18.3 km/h. |  |
Since it's 5.00 km across the river, the time to get across is
| t = x/v = (5.00 km)/(18.3 km/h) = 0.273 h.
|  |
|
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
 railroad station,
railroad station,  west bound train,
west bound train, ground.
So
ground.
So