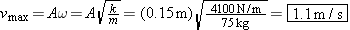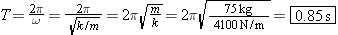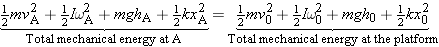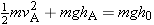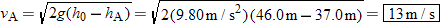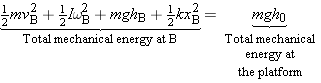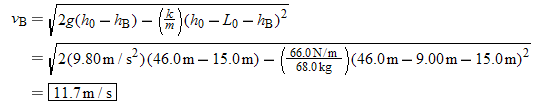|
A 75-kg diver is standing at the end of a diving board while it is vibrating up and down in simple harmonic motion, as indicated in Figure 10.35. The diving board has an effective spring constant of k = = 4100 N/m, and the vertical distance between the highest and lowest points in the motion is 0.30 m. (a) What is the amplitude of the motion? (b) Starting when the diver is at the highest point, what is his speed one-quarter of a period later? (c) If the vertical distance between his highest and lowest points were doubled to 0.60 m, what would be the time required for the diver to make one complete motional cycle? 4100 N/m, and the vertical distance between the highest and lowest points in the motion is 0.30 m. (a) What is the amplitude of the motion? (b) Starting when the diver is at the highest point, what is his speed one-quarter of a period later? (c) If the vertical distance between his highest and lowest points were doubled to 0.60 m, what would be the time required for the diver to make one complete motional cycle?
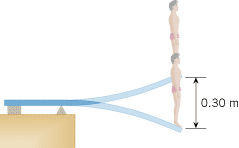 | | Figure 10.35
A diver at the end of a diving board is bouncing up and down in simple harmonic motion. |
|
Concept Questions and Answers How is the amplitude A related to the vertical distance between the highest and lowest points of the diver’s motion?
 | Answer
The amplitude is the distance from the midpoint of the motion to either the highest or the lowest point. Thus, the amplitude is one-half the vertical distance between the highest and lowest points in the motion.
|
Starting from the top, where is the diver located one-quarter of a period later, and what can be said about his speed at this point?
 | Answer
The time for the diver to complete one motional cycle is defined as the period. In one cycle, the diver moves downward from the highest point to the lowest point and then moves upward and returns to the highest point. In a time equal to one-quarter of a period, the diver completes one-quarter of this cycle and, therefore, is halfway between the highest and lowest points. His speed is momentarily zero at the highest and lowest points and is a maximum at the halfway point.
|
If the amplitude of the motion were to double, would the period also double?
 | Answer
No. The period is the time to complete one cycle, and it is equal to the distance traveled during one cycle divided by the average speed. If the amplitude doubles, the distance also doubles. However, the average speed also doubles. We can verify this by examining Equation 10.7, which gives the diver’s velocity as 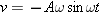 . The speed is the magnitude of this value, or . The speed is the magnitude of this value, or 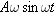 . Since the speed is proportional to the amplitude A, the speed at every point in the cycle also doubles when the amplitude doubles. Thus, the average speed doubles. However, the period, being the distance divided by the average speed, does not change. . Since the speed is proportional to the amplitude A, the speed at every point in the cycle also doubles when the amplitude doubles. Thus, the average speed doubles. However, the period, being the distance divided by the average speed, does not change.
|
Solution
| (a) |
Since the amplitude A is one-half the vertical distance between the highest and lowest points in the motion, 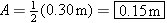 . .
| | (b) |
When the diver is halfway between the highest and lowest points, his speed is a maximum. The maximum speed of an object vibrating in simple harmonic motion is given by Equation 10.8 as vmax = = Aw, where A is the amplitude of the motion and w is the angular frequency. The angular frequency can be determined from Equation 10.11 as Aw, where A is the amplitude of the motion and w is the angular frequency. The angular frequency can be determined from Equation 10.11 as 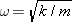 , where k is the effective spring constant of the diving board and m is the mass of the diver. The maximum speed is , where k is the effective spring constant of the diving board and m is the mass of the diver. The maximum speed is
| | (c) |
The period is the same, regardless of the amplitude of the motion. From Equation 10.4 we know that the period T and the angular speed w are related by T = = 2p/w, where 2p/w, where 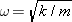 . Thus, the period can be written as
As expected, the period does not depend on the amplitude of the motion. . Thus, the period can be written as
As expected, the period does not depend on the amplitude of the motion.
|
|
![]() =
=![]() 4100 N/m, and the vertical distance between the highest and lowest points in the motion is 0.30 m. (a) What is the amplitude of the motion? (b) Starting when the diver is at the highest point, what is his speed one-quarter of a period later? (c) If the vertical distance between his highest and lowest points were doubled to 0.60 m, what would be the time required for the diver to make one complete motional cycle?
4100 N/m, and the vertical distance between the highest and lowest points in the motion is 0.30 m. (a) What is the amplitude of the motion? (b) Starting when the diver is at the highest point, what is his speed one-quarter of a period later? (c) If the vertical distance between his highest and lowest points were doubled to 0.60 m, what would be the time required for the diver to make one complete motional cycle?
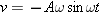 . The speed is the magnitude of this value, or
. The speed is the magnitude of this value, or 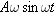 . Since the speed is proportional to the amplitude A, the speed at every point in the cycle also doubles when the amplitude doubles. Thus, the average speed doubles. However, the period, being the distance divided by the average speed, does not change.
. Since the speed is proportional to the amplitude A, the speed at every point in the cycle also doubles when the amplitude doubles. Thus, the average speed doubles. However, the period, being the distance divided by the average speed, does not change.
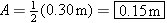 .
.
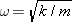 , where k is the effective spring constant of the diving board and m is the mass of the diver. The maximum speed is
, where k is the effective spring constant of the diving board and m is the mass of the diver. The maximum speed is
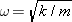 . Thus, the period can be written as
. Thus, the period can be written as