The Ideal Spring and Simple Harmonic Motion

10.1. The Ideal Spring and Simple Harmonic Motion

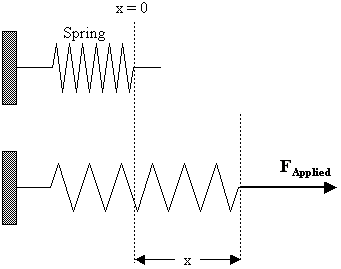
Consider the following figure in which an unstretched spring is pulled on by a force F _Applied. In the process, the spring will be stretched by an amount x from its unstrained or equilibrium position (x = 0).

For relatively small deformations, the force required to stretch (or compress) the spring obeys the following equation:

F _Applied = kx

(10.1)

The constant k is called the spring constant which is a measure of the stiffness of the spring (units for k are N/m). The larger the value of k, the harder it is to stretch the spring. Any spring that obeys equation (10.1) is said to be an ideal spring.

To stretch or compress a spring, a force must be applied to it. As a consequence of Newton's third law, the spring must exert an oppositely-directed force of equal magnitude. The force of the spring is a "restoring force" in the sense that it tries to pull or push the spring back to its equilibrium (x = 0) position. This restoring force can thus be written

F = - kx

(10.2)

The minus sign means that the restoring force always points in a direction opposite to the direction of deformation.

Example 1

A spring has a spring constant of 155 N/m. What is the magnitude of the force needed (a) to stretch the spring by 5.00 cm from its unstretched length and (b) to compress the spring by the same amount?

(a)

Using equation (10.1) we have:

F _Applied = kx = (155 N/m)(5.00 × 10^-2 m) = 7.75 N.

(b)

The magnitude of the force required to compress the spring by the same amount (5.00 cm) is EXACTLY the same as that found in part (a), 7.75 N. That is, the same force is needed for stretching or compressing the spring by equal amounts. The difference lies in the direction of the force.

Imagine that we now attach one end of a spring to a wall, and the other end to a block which rests on a horizontal frictionless surface, as shown in the figure below. If we were to pull the block to the right, stretching the spring, and then let go, what would happen? The restoring force, given by equation (10.2), would act to pull the block back to the left. The block would begin to move to the left. However, because of the block's momentum it would not stop when it returned to its equilibrium position. It would continue to move until the spring compressed enough to stop the block. The restoring force of the spring would now push the block back to the right, and again it would begin to move (this time to the right). As it passed through its equilibrium position it would keep moving until stopped by the force of the once again stretched spring. The process would then repeat, over and over again. This is referred to as Simple Harmonic Motion.

For an ideal spring, and on a frictionless surface, the block will continue to oscillate back and forth forever. We can describe this oscillatory motion by first defining a number of important quantities that are basic to any type of repetitive motion. This follows in the next section.