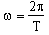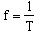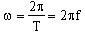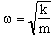10.2.
Simple Harmonic Motion and the Reference Circle
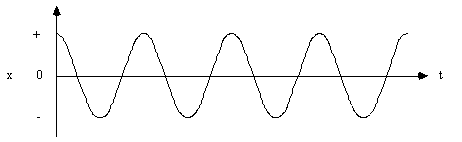
If we were to plot the motion depicted in the above figure, that is, the displacement of the block x as a function of time t, we would obtain the following graph. Note that a displacement of the block to the right of the equilibrium position is positive (+) and a displacement to the left of x = 0 is negative (-).
The graph above shows that the displacement is represented by a cosine function which can be expressed as
| x = A cos wt | (10.3) |  |
In equation (10.3), A is called the amplitude of the motion, that is, the magnitude of the maximum x-displacement of the block from its equilibrium position. The quantity, w is the angular frequency where
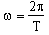 | (10.4) |  |
and T is the period, the time required for the block to complete one cycle of its motion. A related quantity is the frequency, which represents the number of cycles of motion completed each second. We have
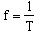 | (10.5) |  |
The frequency has a unit of s-1 which is referred to as one hertz (Hz). Finally, the angular frequency is written
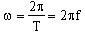 | (10.6) |  |
The velocity of the block can also be represented by a sinusoidally varying function. We can write
| v = - Aw sin q = - Aw sin wt | (10.7) |  |
Note the negative sign in equation (10.7). This is needed because the block begins to move to the left initially (i.e., in the negative x direction). The block's velocity is zero at each end point of its motion and it reaches its maximum value (+ or -) at the equilibrium position, x = 0. The maximum of equation (10.7) occurs when sin wt = ± 1. So,
| vmax = Aw (w in rad/s) | (10.8) |  |
In simple harmonic motion, the velocity is NOT constant, therefore, there IS acceleration. Furthermore, since the force varies as a function of x (i.e., the more you stretch the spring, the harder it becomes to keep it stretched), the acceleration is not constant either. The acceleration of the block can be written as
| a = - Aw
2 cos q = - Aw
2 cos wt | (10.9) |  |
The acceleration is zero at x = 0 (since F = - kx = ma = 0 because x = 0) and reaches its maximum value at the endpoints of its motion (i.e., when x = A). The expression for amax
is obtained by setting cos wt = ± 1 in the above equation (10.9). We therefore have,
| amax = Aw
2 (w in rad/s) | (10.10) |  |
Finally, it can be shown that the angular frequency is related to the mass of the block, m, and the stiffness of the spring, k, by the equation
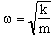 | (10.11) |  |
Example 2
A spring whose spring constant is 196 N/m is attached to a block of mass 5.00 kg which sits on a horizontal, frictionless surface. The block is pulled 20.0 cm to the side and released. Find (a) the frequency, (b) the period, (c) the amplitude, (d) the maximum velocity, and (e) the maximum acceleration of the block; (f) write expressions for the displacement, velocity, and acceleration of the block as a function of time.
| (a) | Using equation (10.11),
Using equation (10.6),
|
| (b) | Using equation (10.5),
|
| (c) | The amplitude is,
| A = 20.0 cm = 0.200 m |  |
|
| (d) | Using equation (10.8),
|
| (e) | Using equation (10.10),
|
| (f) | Using equations (10.3), (10.7), and (10.9), and the values of A and w found above, we can write
| x = A cos wt = (0.200)[cos (6.26t)] m |  |
| v = - Aw sin wt = - (0.200 m)(6.26 rad/s)[sin (6.26t)] |  |
| = - (1.25)[sin (6.26t)] m/s |  |
| a = - Aw
2 cos wt = - (0.200 m)(6.26 rad/s)2 [cos (6.26 t)] |  |
| = - (7.84)[cos (6.26t)] m/s2. |  |
|
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |