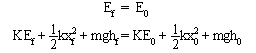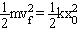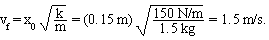10.3.
Energy and Simple Harmonic Motion
When an object is attached to a spring, the spring force can do work Welastic
on the object. If in addition, nonconservative forces do work Wnc
on the object, the work-energy theorem discussed in Chapter 6 states that this work will result in a change in energy for the system. This can be stated mathematically as
| Wnc + Welastic = DKE + DPEgrav
|  |
The work required to stretch a spring from its initial position x0
to its final position xf, is given by
| Welastic = 1/2 kx0
2 - 1/2 kxf
2
| (10.12) |  |
The work done to stretch the spring therefore gives rise to a change in the elastic potential energy of the spring. In general, if a spring is stretched (or compressed) by an amount x, we can write
| PEelastic = 1/2 kx2
| (10.13) |  |
In the special case where only the forces of the spring and gravity are present, the total mechanical energy of the system, E, can be written
| E = KE + PEgrav + PEelastic
|  |
Example 3
A spring (spring constant 150 N/m) is attached to a 1.5 kg block which rests on a horizontal frictionless surface. If the block is set in motion and oscillates with an amplitude of 15 cm, what is the velocity of the block as it passes through its equilibrium position?
The conservation of energy principle states that, in the absence of friction or air resistance, the total mechanical energy of the system is conserved. That is
Since the spring is horizontal, there is no change in PEgrav
since hf = h0. Take the initial position to be when the spring is fully stretched, and the final position to be the equilibrium position. We can make the following substitutions: x0 = A = 0.15 m, xf = 0, v0 = 0. We are therefore left with
and we can solve for the final velocity,
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |