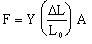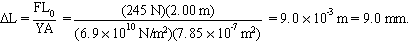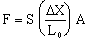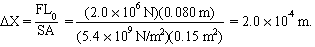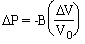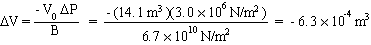10.7.
Elastic Deformation
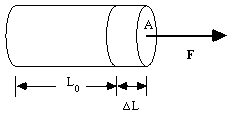
Refer to the following figure in which an object of length L0
and cross-sectional area A is subjected to a force, F, which pulls (or pushes) along the length of the object (i.e., perpendicular to A). The object will stretch (or compress) by an amount DL as shown in the figure.
If the amount of stretching is small compared to the original length of the object, the elastic behavior of the material is maintained. We must incorporate a proportionality constant (which depends on the type of material being stretched) which relates the fractional change in length (DL/L0) to the force per unit area (F/A) being applied, i.e.,
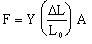 | (10.17) |  |
Here, the proportionality constant, Y, is known as Young's Modulus. Solving equation (10.17) for Y shows that Young's modulus has units of force per unit area (N/m2); the exact value depends on the nature of the material.Example 5
A 25.0 kg mass is suspended from an aluminum wire of length 2.00 m and diameter 1.00 mm. By how much does the wire stretch?
The cross-sectional area of the wire is
| A = pr2 = p(5.00 × 10-4 m)2 = 7.85 × 10-7 m2. |  |
The force being applied is the weight of the 25.0 kg mass, i.e.,
| F = mg = (25.0 kg)(9.80 m/s2) = 245 N. |  |
Using Table 10.1 we look up the value of Young's modulus for aluminum. We find Y = 6.9 × 1010 N/m2. The amount the wire stretches is therefore,
It is possible to deform a solid object in a way other than stretching or compressing it. Suppose a force is applied parallel to the cross-sectional area of the object, as shown in the figure below.
The resulting deformation in the material is called a shear deformation. The magnitude of the force F needed to produce an amount of shear
DX for an object of cross-sectional area A and thickness L0
is given by
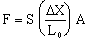 | (10.18) |  |
The constant of proportionality, S, is known as the shear modulus. Like Young's modulus, it has units of force per unit area (N/m2), and depends on the nature of the material.
Example 6
A lead block of length 0.50 m, width 0.30 m, and height 0.080 m is subjected to a shearing force of 2.0 × 106 N directed perpendicular to its height. The shear modulus for lead (from Table 10.2) is S = 5.4 × 109 N/m2. Find the amount of shear,
DX.
Using equation (10.18) with A = length ×width = (0.50 m)(0.30 m) = 0.15 m2
and L0 = height = 0.080 m, we have
When a compressive force is applied to all three dimensions of a solid, the length of each dimension decreases, leading to a decrease in volume for the object. The forces acting in such situations are applied perpendicular to every available surface. Because of this, we speak of the perpendicular force per unit area, rather than the total force involved. The perpendicular force per unit area is called the pressure. When such a pressure is applied to a volume V, the volume changes by an amount
DV, according to the relation
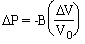 | (10.20) |  |
The proportionality constant, B, is known as the bulk modulus of the material. The minus sign appears in equation (10.20) because an increase in pressure (DP positive) always results in a decrease in volume (DV negative). B is always a positive quantity.
Example 7
A brass sphere of radius 1.50 m is subjected to a pressure increase of 3.0 × 106 N/m2. What change in volume results?
The volume of the sphere is
| V = (4/3)pr3 = (4/3)p(1.50 m)3 = 14.1 m3. |  |
The bulk modulus for brass (obtained from Table 10.3) is B = 6.7 × 1010 N/m2. The change in volume is therefore
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |