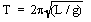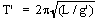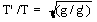PRACTICE PROBLEMS

A 2.0 kg block hung from a vertical spring causes it to stretch by 20.0 cm. If the 2.0 kg block is replaced by a 0.50 kg mass, and the spring is stretched and released, what are the frequency and period of the oscillations?

Find the spring constant using equation (10.1), F_Applied = kx which gives

k = FApplied/x = (2.0 kg)(9.8 m/s2)/(0.20 m) = 98 N/m.

f = w/2p = 2.2 Hz.

T = 1/f = 0.45 s.

A small object of mass 0.20 kg is undergoing simple harmonic motion of period 0.80 s and amplitude 0.50 m. (a) What is the maximum force acting on the object? (b) What is the maximum velocity of the object? (c) If the oscillations are produced by a spring, what is the force constant of the spring?

(a)	The maximum acceleration, equation (10.10), is amax = Aw 2 = A(2p/T)2 amax = (0.50 m)[2p/(0.80 s)]2 amax = 31 m/s2. The maximum force is obtained from Fmax = mamax = (0.20 kg)(31 m/s2) = 6.2 N.
(b)	Using equation (10.8), vmax = Aw = A(2p/T) = (0.50 m)[2p/(0.80 s)] = 3.9 m/s.
(c)	Using FApplied = kx k = FApplied/x = (6.2 N)/(0.50 m) = 12 N/m.

A 16-lb object hangs from a spring. It undergoes simple harmonic motion in a vertical direction with an amplitude of 6.0 in and a frequency of 2.0 Hz. Find (a) the period, (b) the force constant of the spring, (c) the maximum speed of the object, (d) the maximum acceleration of the object, (e) the speed when the object is at half its maximum displacement.

(a)	Equation (10.5), T = 1/f = 1/(2.0 Hz) = 0.50 s,
(b)	Equation (10.6), solving for k, k = 4p 2f2m = 4p 2(2.0 Hz)2(0.5 slugs) = 79 lb/ft,
(c)	vmax = Aw = A(2pf) = (0.5 ft)(2p)(2.0 Hz) = 6.3 ft/s,
(d)	amax = Aw 2 = (0.5 ft)[2p(2.0 Hz)]2 = 79 ft/s2 ,
(e)	Using conservation of energy, (1/2)kA2 = (1/2)k(A/2)2 + (1/2)mv2. Thus, v2 = (3/4)kA2/m = (3/4)(79 lb/ft)(0.5 ft)2/(0.5 sl), or v = 5.4 ft/s.

A 1200 kg car oscillates vertically on its suspension springs with a period of 0.60 s when empty. If six persons, each of mass 80.0 kg, get into the car, how far down will the supporting springs be depressed?

Find the spring constant using equation (10.11),

k = mw 2 = (1200 kg)[2p/(0.6 s)]2 = 1.3 × 105 N/m.

x = FApplied /k = 6(80.0 kg)(9.80 m/s2)/(1.3 × 105 N/m) = 3.6 cm.

A block of mass 0.10 kg is placed on top of a block of mass 0.20 kg. The coefficient of static friction between the blocks is 0.20. The lower block is now moved back and forth horizontally in simple harmonic oscillations with an amplitude of 6.0 cm. Keeping the amplitude constant, what is the highest frequency for which the upper block will not slip relative to the lower block?

The force of static friction for the top block (m₁) is

fs = m m 1g = (0.20)(0.10 kg)(9.8 m/s2) = 0.20 N.

amax = fs/m = (0.20 N)/(0.10 kg) = 2.0 m/s2

amax = Aw 2 = A(2pf)2

f2 = amax/4p 2A = (2.0 m/s2)/[4p 2(0.06 m)],

f = 0.92 Hz.

A pendulum clock keeps perfect time at a location where the acceleration due to gravity is exactly 9.80 m/s². When the clock is moved to a higher altitude, it loses 80.0 s per day. Find the value of g at this new location.

If the clock loses 80.0 s per day, it must be swinging slower (T greater). It loses (80.0 s/86 400 s) = 0.926 ms each second. Therefore, the new period is 1.000 926 s. If the original period is

g' = g (T/T')2 = (9.80 m/s2)[(1.000 s)/(1.001 s)]2 = 9.78 m/s2 .

A spring (spring constant of 2500 N/m) is fixed vertically to the floor. A 10.0 kg ball is placed on the spring, pushed down 0.50 m, and released. How high does the ball fly above its release position?

Using conservation of energy,

EA = (1/2)kx2 = EB = mgh.

h = kx2/2mg = (2500 N/m)(0.5 m)2/[2(10.0 kg)(9.80 m/s2)] = 3.2 m.

A steel wire can withstand a tensile stress of 6.0 × 10⁸ N/m². If such a wire is used to support a mass of 750 kg, what is the minimum diameter wire that can be used?

We know that stress = F/A where A = (1/4)pd² and d = diameter. Solving for d we obtain

d2 = 4F/[p(stress)] = 4(750 kg)(9.80 m/s2)/[p(6.0 × 108 N/m2)]

d = 3.9 × 10-3 m.

A copper sphere is subjected to a pressure of 2.0 × 10¹⁰ Pa. What is the resulting fractional change in the volume of the sphere? What is the fractional change in the sphere's radius?

Using equation (10.20),

DP = -B( DV/V0).

( DV/V0) = DP/B = (2.0 × 1010 Pa)/(1.3 × 1011 Pa) = 1.5 × 10-1 .

(Dr/r0) = (1/3)( DV/V0) = 5.0 × 10-2 .

A rectangular block of tungsten is 5.00 cm high and has a cross-sectional a a of 144 cm². A force of 3.6 × 10⁷ N is applied to the block. (a) If the force pushes perpendicular to the block's area, by how much will the block compress? (b) If the force is applied parallel to the surface (i.e., a shearing force), what will the amount of shear deformation be?

(a)	Equation (10.17), DL = FL0/YA = (3.6 × 107 N)(5.00 × 10-2 m)/[(3.6 × 1011 Pa)(144 × 10-4 m2)] DL = 0.35 mm
(b)	Equation (10.18), DX = FL0/SA = (3.6 × 107 N)(5.00 × 10-2 m)/[(1.5 × 1011 Pa)(144 × 10-4 m2)] DX = 0.83 mm

Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved.