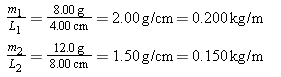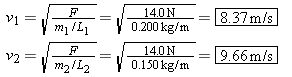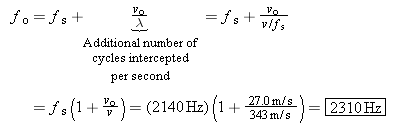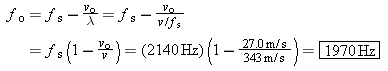|
A siren, mounted on a tower, emits a sound whose frequency is 2140 Hz. A person is driving a car away from the tower at a speed of 27.0 m/s. As Figure 16.39 illustrates, the sound reaches the person by two paths: the sound reflected from a building in front of the car, and the sound coming directly from the siren. The speed of sound is 343 m/s. What frequency does the person hear for the (a) reflected and (b) direct sounds?
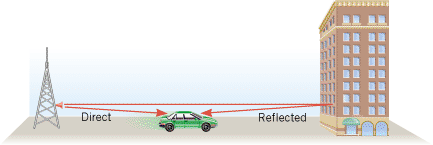 | | Figure 16.39
The sound from the siren reaches the car by a reflected path and a direct path. The direct and reflected sound waves, as well as the motion of the car, are assumed to lie along the same line. Because of the Doppler effect, the driver hears a different frequency for each sound. |
|
Concept Questions and Answers One way that the Doppler effect can arise is that the wavelength of the sound changes. For either the direct or the reflected sound, does the wavelength change?
 | Answer
No. The wavelength changes only when the source of the sound is moving, as illustrated in Figure 16.30b. The siren is stationary, so the wavelength does not change.
|
Why does the driver hear a frequency for the reflected sound that is different than 2140 Hz, and is it greater than or smaller than 2140 Hz?
 | Answer
The car and the reflected sound are traveling in opposite directions, the car to the right and the reflected sound to the left. The driver intercepts more wave cycles per second than if the car were stationary. Consequently, the driver hears a frequency greater than 2140 Hz.
|
Why does the driver hear a frequency for the direct sound that is different than 2140 Hz, and is it greater than or smaller than 2140 Hz?
 | Answer
The car and the direct sound are traveling in the same direction. As the sound passes the car, the number of wave cycles per second intercepted by the driver is now less than if the car were stationary. Thus, the driver hears a frequency that is less than 2140 Hz.
|
Solution
| (a) |
For the reflected sound, the frequency fo that the driver (the “observer”) hears is equal to the frequency fs of the waves emitted by the siren plus an additional number of cycles per second because the car and the reflected sound are moving in opposite directions. The additional number of cycles per second is vo/l, where vo is the speed of the car and l is the wavelength of the sound (see the subsection “Moving Observer” in Section 16.9). According to Equation 16.1, the wavelength is equal to the speed of sound v divided by the frequency of the siren, l = = v/fs. Thus, the frequency heard by the driver can be written as v/fs. Thus, the frequency heard by the driver can be written as
| | (b) |
For the direct sound, the frequency fo that the driver hears is equal to the frequency fs of the waves emitted by the siren minus vo/l, because the car and direct sound are moving in the same direction:
As expected, for the reflected wave, the driver hears a frequency greater than 2140 Hz, while for the direct sound he hears a frequency less than 2140 Hz.
|
|

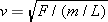 , where F is the tension and m/L is the mass per unit length, or linear density. Since both strings support the box, the tension in each is one-half the weight of the box, or
, where F is the tension and m/L is the mass per unit length, or linear density. Since both strings support the box, the tension in each is one-half the weight of the box, or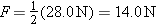 . The linear densities of the strings are
. The linear densities of the strings are