Note: Each of these problems consists of Concept Questions followed by a related quantitative Problem. They are designed for use by students working alone or in small learning groups. The Concept Questions involve little or no mathematics and are intended to stimulate group discussions. They focus on the concepts with which the problems deal. Recognizing the concepts is the essential initial step in any problem-solving technique.
| 103 | |
| ||
| ||
Concept Questions The drawing shows a snapshot of two waves traveling to the right at the same speed. (a) Rank the waves according to their wavelengths, largest first. (b) Which wave, if either, has the higher frequency? (c) If a particle were attached to each wave, like that in Figure 16.10, which particle would have the greater maximum speed as it moves up and down? Justify your answers.
Problem (a) From the data in the drawing, determine the wavelength of each wave. (b) If the speed of the waves is 12 m/s, calculate the frequency of each one. (c) What is the maximum speed for a particle attached to each wave? Check that your answers are consistent with those for the Concept Questions.
 |
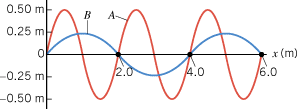| 104 | |
| ||
| ||
Concept Questions Example 4 in the text discusses an ultrasonic ruler that displays the distance between the ruler and an object, such as a wall. The ruler sends out a pulse of ultrasonic sound and measures the time it takes for the pulse to reflect from the object and return. The ruler uses this time, along with a preset value for the speed of sound in air, to determine the distance. Suppose you use this ruler underwater, rather than in air. (a) Is the speed of sound in water greater than, less than, or equal to the speed of sound in air? (b) Is the reading on the ruler greater than, less than, or equal to the actual distance? Provide reasons for your answers.
Problem The actual distance from the ultrasonic ruler to an object is 25.0 m. The adiabatic bulk modulus and density of seawater are Bad=2.31×109 Pa and r=1025 kg/m3, respectively. Assume that the ruler uses a preset value of 343 m/s for the speed of sound in air, and determine the distance reading on its display. Verify that your answer is consistent with your answers to the Concept Questions.
| 105 | |
| ||
| ||
Concept Questions Suppose you are part of a team that is trying to break the sound barrier with a jet-powered car, which means that it must travel faster than the speed of sound in air. Would you attempt this feat early in the morning when the temperature is cool, later in the afternoon when the temperature is warmer, or does it even matter what the temperature is?
Problem In the morning, the air temperature is 0 °C and the speed of sound is 331 m/s. What must be the speed of your car if it is to break the sound barrier when the temperature has risen to 43 °C in the afternoon? Assume that air behaves like an ideal gas.
| 106 | |
| ||
| ||
Concept Questions A source of sound is located at the center of two concentric spheres, parts of which are shown in the drawing. The source emits sound uniformly in all directions. On the spheres are drawn three small patches that may, or may not, have equal areas. However, the same sound power passes through each patch. (a) Rank the sound intensity at each patch, greatest first. (b) Rank the area of each patch, largest first. Provide reasons for your answers.
Problem The source produces 2.3 W of sound power, and the radii of the concentric spheres are rA=0.60 m and rB=0.80 m. (a) Determine the sound intensity at each of the three patches. (b) The sound power that passes through each of the patches is 1.8×10–3 W. Find the area of each patch. Verify that your answers are consistent with those to the Concept Questions.
 |
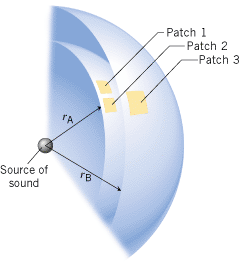| 107 | |
| ||
| ||
Concept Questions The threshold of hearing for an average young person is 0 dB. Two individuals who are not average have thresholds of hearing that are b1=–8.00 dB and b2=+12.0 dB. (a) Is the sound intensity at a level of –8.00 dB greater than, or less than, that at 0 dB? (b) Which individual has the better hearing? Why?
Problem How many times greater (or less) is the sound intensity when person 1 (b1=–8.00 dB) hears it at the threshold of hearing compared to when person 2 (b2=+12.0 dB) hears it at the threshold of hearing? Check to see that your answer is consistent with your answers to the Concept Questions.
| 108 | |
| ||
| ||
Concept Questions The table shows three situations in which the Doppler effect may arise. The first two columns indicate the velocities of the sound source and the observer, where the length of each arrow is proportional to the speed. For each situation, fill in the empty columns by deciding whether the wavelength of the sound and the frequency heard by the observer increase, decrease, or remain the same compared to the case when there is no Doppler effect. Provide a reason for each answer.
|
|
Velocity of Sound Source (Toward the Observer) |
Velocity of Observer (Toward the Source) |
Wavelength |
Frequency Heard by Observer | |
| |||||
|
(a) |
0 m/s |
0 m/s |
|
|
|
|
(b) |
 |
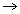0 m/s |
|
|
|
|
(c) |
|
 |
|
|
|
| |||||
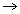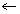Problem The siren on an ambulance is emitting a sound whose frequency is 2450 Hz. The speed of sound is 343 m/s. (a) If the ambulance is stationary and you (the “observer”) are sitting in a parked car, what is the wavelength of the sound and the frequency heard by you? (b) Suppose the ambulance is moving toward you at a speed of 26.8 m/s. Determine the wavelength of the sound and the frequency heard by you. (c) If the ambulance is moving toward you at a speed of 26.8 m/s and you are moving toward it at a speed of 14.0 m/s, find the wavelength of the sound and the frequency that you hear. Be sure that your answers are consistent with your answers to the Concept Questions.
| 109 | |
| ||
| ||
Concept Questions A uniform rope of mass m and length L is hanging straight down from the ceiling. (a) Is the tension in the rope greater near the top or near the bottom of the rope? Why? (b) A small-amplitude transverse wave is sent up the rope from the bottom end. Is the speed of the wave greater near the bottom or near the top of the rope? Explain. (c) Consider a section of the rope between the bottom end and a point that is a distance y meters above the bottom. What is the weight of this section? Express your answer in terms of m, L, y, and g (the acceleration due to gravity).
Problem (a) For the rope described in the Concept Questions, derive an expression that gives the speed of the wave on the rope in terms of the distance y above the bottom end and the acceleration g due to gravity. (b) Use the expression that you have derived to calculate the speeds at distances of 0.50 m and 2.0 m above the bottom end of the rope. Be sure that your answers are consistent with your answer to Concept Question (b).
| 110 | |
| ||
| ||
Concept Questions A wireless transmitting microphone is mounted on a small platform, which can roll down an incline, away from a speaker that is mounted at the top of the incline. The speaker broadcasts a fixed-frequency tone. (a) The platform is positioned in front of the speaker and released from rest. Describe how the velocity of the platform changes and why. (b) How is the changing velocity related to the acceleration of the platform? (c) Describe how the frequency detected by the microphone changes. Explain why the frequency changes as you have described. (d) Which equation given in the chapter applies to this situation? Justify your answer.
Problem The speaker broadcasts a tone that has a frequency of 1.000×104 Hz, and the speed of sound is 343 m/s. At a time of 1.5 s following the release of the platform, the microphone detects a frequency of 9939 Hz. At a time of 3.5 s following the release of the platform, the microphone detects a frequency of 9857 Hz. What is the acceleration (assumed constant) of the platform?
|