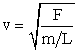
16.3.
The Speed of a Wave on a String
The speed of transverse waves on a string of uniform linear density is
Example 4
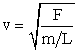A string of linear density, 2.0 g/m, is stretched to a tension of 4.9 N. What is the speed of the waves on the string? If the tension is increased so that the speed of the waves doubles, what is the new tension?
Solving the above equation for the tension results in
| F = (m/L)v2
|  |
If the speed of the waves doubles to 2v, then the new tension is
| F' = 4 (m/L)v2 = 4F = 2.0 × 101 N | |
Example 5
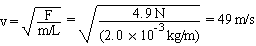A uniform wire carries waves whose frequency and wavelength are 450 Hz and 1.2 m, respectively. If the string is known to be under a tension of 250 N, what is the linear density of the wire?
The linear density can be found from equation (16.2): m/L = F/v2.
The speed of the waves on the wire can be found from v = lf = (1.2 m)(450 Hz) = 540 m/s, so
| m/L = (250 N)/(540 m/s)2 = 8.57 × 10- 4 kg/m. | |
|
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
