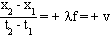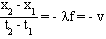The Mathematical Description of a Wave

16.4. The Mathematical Description of a Wave

If a periodic wave results from simple harmonic motion at the source, then, ideally, EACH point in the medium oscillates with simple harmonic motion. The displacement at a particular point, x = 0 (time view) is y = A sin (2pft). As we saw before, the wave frozen in time looks like a sine wave, too. The displacement of each point at time zero (space view) can be written y = A sin ( ± 2px/l). It is customary to combine the space and time views into a single equation

y = A sin (2pft - 2px/l)

for a wave traveling towards +x and

y = A sin (2pft + 2px/l)

for a wave traveling towards -x.

Example 6

Show that equation (16.3) represents a wave traveling toward +x and that equation (16.4) represents a wave traveling toward -x.

Imagine watching a single point on a wave as it travels. This point appears to move with the speed of the wave and always has the same displacement. That is, the value of the sine function is constant. The only way for a sine function to remain constant is for its argument (the angle) to remain constant. Equation (16.3) then gives 2pft - 2px/l = C, a constant. At some time, t₁, the point has a position, x₁, so 2pft₁ - 2px₁/l = C. At a later time, t₂, the point has a new position, x₂, so 2pft₂ - 2px₂/l= C. Subtracting and rearranging yields the velocity of the point on the wave

which is positive, indicating that the wave is traveling toward +x. A similar treatment using equation (16.4) gives

which is negative. This wave is traveling toward the -x direction. Example 7

The wave traveling on the string in example 4 has a wavelength of 0.50 m and an amplitude of 2.5 mm. Write an equation describing the wave as it travels toward the +x axis.

Equation (16.3) applies to a wave traveling toward +x. We need to find the frequency.

f = v/l = (49 m/s)/(0.50 m) = 98 Hz.

Now

y = A sin (2pft - 2px/l) = (2.5 mm) sin [2p(98 s^{- 1})t - 2px(2.0 m^{- 1})]

where x is in meters and t is in seconds. Example 8

What are the wavelength, frequency and speed of the wave described by

y = (5.0 mm) sin [(450 s^{- 1})t - (25 m^{- 1})x]?

Comparing our wave with equation (16.3) shows that 2pf = 450 s^{- 1} and 2p/l = 25 m^{- 1}, so

f = 72 Hz and l= 0.25 m

The speed of the wave is then

v = lf = 18 m/s.