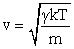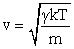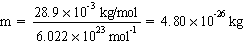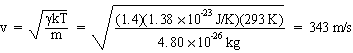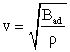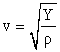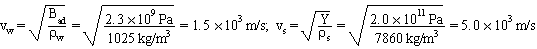16.6.
The Speed of Sound
Sound travels through different materials at different speeds. For example, at room temperature sound travels at about 343 m/s in air. However, sound travels at about 1482 m/s through water and 5960 m/s through bulk steel at the same temperature. In general, sound travels slowest in gases, faster in liquids, and fastest in solids.
For a gas, the speed of sound depends on the temperature of the gas, and the type of molecules making up the gas. If we consider the situation for an ideal gas, we find that the speed of sound in that gas can be written
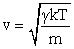 | (16.5) |  |
where
g = cP/cV
is the ratio of specific heat capacity at constant pressure to the specific heat capacity at constant volume, m is the mass of a molecule of the gas, k is Boltzmann's constant, and T is the Kelvin temperature.
Example 9
Determine the speed of sound in air at 20.0 °C assuming the mean molecular mass of air to be 28.9 × 10-3 kg/mol and the ratio of specific heats to be
g = 1.4.
First we need to find the mass of an air molecule based on the mean molecular mass and Avogadro's number.
Now use equation (16.5) to determine the speed of sound in air
In a liquid, the speed of sound depends on the density of the material r and the adiabatic bulk modulus Bad:
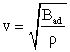 | (16.6) |  |
In a solid, in the shape of a long slender bar, the speed of sound depends on the density and Young's modulus for the material:
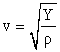 | (16.7) |  |
Example 10
A steel rod extends 2500 m under the ocean water. A sound is produced at one end of the rod and travels through both the rod and the water. What is the delay time between the arrival of the sound waves in the rod and the water? Take the bulk modulus for sea water to be Bad = 2.3 × 109 Pa, the density of sea water to be
r
w = 1025 kg/m3, Young's modulus for steel to be Y = 2.0 × 1011 Pa, and the density of steel to be
r
s = 7860 kg/m3.
The time it takes for each sound to travel 2500 m can now be calculated:
Therefore, the delay time between the arrival of the two waves is
|
Dt = tw - ts = 1.7 s - 0.50 s = 1.2 s. |  |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |