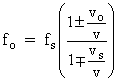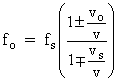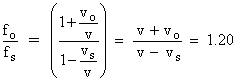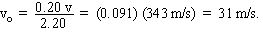The Doppler Effect

16.9. The Doppler Effect

When a source of sound is in motion, or when a listener is moving, the frequency of the sound that is observed will change. This effect, known as the Doppler effect, is the change in pitch or frequency of the sound detected by an observer because the sound source and the observer have different velocities with respect to the medium of sound propagation. For example, when you hear the siren of an approaching fire truck you notice a definite change in pitch of the siren as it passes. As the truck approaches, the pitch is relatively high (that is, the frequency is high). However, as the truck passes you and moves away, the pitch drops (frequency lowers).

Let f_s represent the frequency of the sound emitted by a source. Sound travels at a speed v in the particular medium of propagation. The source may be moving with a speed v_s, and the observer may be moving with a speed v_o. The frequency observed, f_o, will be different from the emitted frequency according to the relation

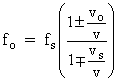(16.15)

In the numerator of the equation, the plus sign applies when the observer moves toward the source, and the minus sign applies when the observer moves away from the source. In the denominator, the minus sign is used when the source moves toward the observer, and the plus sign is used when the source moves away from the observer. The symbols v, v_o, and v_s denote numbers without algebraic sign, because the direction of travel has been taken into account by the plus and minus signs that appear directly in the equation.

Example 13

Two trucks travel at the same speed. They are far apart on adjacent lanes and thus, approach each other essentially head-on. One driver hears the horn of the other truck at a frequency that is 1.20 times the frequency he hears when the trucks are stationary. The speed of sound is 343 m/s. At what speed is each truck moving?

In this particular problem, the observer and source move with the same speed, so v_o = v_s . If the observed frequency is 1.20 times the emitted frequency, then f_o / f_s = 1.20. Equation (16.15) then yields

Note that the plus sign was used in the numerator (since the observer is approaching the source) and a minus sign was used in the denominator (since the source is approaching the observer). Solving for v_o leads to

v + v_o = 1.20 (v - v_o)

which gives

2.20 v_o = 0.20 v.

Thus, in order for the frequency to increase by a factor of 1.20, the observer and source are each moving at 31 m/s along the road.