Chapter Summary
PREVIEW
This is the first of two chapters covering waves. In this chapter you will become acquainted with the concept of waves, in particular a special wave referred to as a periodic wave. You will learn to describe a periodic wave in space by its wavelength and amplitude and in time by its amplitude and period. Combining these descriptions allows us to find the speed of a wave in terms of its frequency and wavelength. The speed of waves on a stretched string will be investigated. A mathematical description of harmonic waves is given. This is very important since any complicated wave can be described as a sum of harmonic waves, as you will learn in a later chapter.
In this chapter you will also study the nature of sound. The wave properties of sound are examined, including the speed of sound in gases, liquids, and solids. You will be introduced to the concepts of sound intensity, loudness, and the decibel scale. Applications of sound are also discussed, such as sonar, ultrasound, and the Doppler effect.
QUICK REFERENCE
Important Terms
Equations
The speed of a periodic wave which has a wavelength, l, and a frequency, f, is
The speed of a wave traveling on a string under a tension, F, and having a linear density m/L is
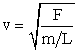 |
The displacement of a particle of the medium from its undisturbed position when a harmonic wave is moving along the
The speed of sound in a gas is:
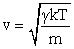 |
The speed of sound in a liquid is:
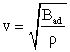 |
The speed of sound in a long, thin, solid bar is:
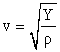 |
The sound intensity is defined as:
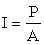 |
If a sound is emitted uniformly in all directions, the intensity at a distance r from the source is:
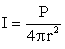 |
The intensity level in decibels is defined as:
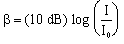 |
The Doppler shifted frequency (general case) is:
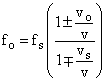 |