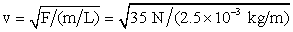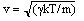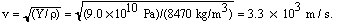PRACTICE PROBLEMS

A light wave has a wavelength of 4.55 × 10^{- 7} m and travels with a speed of 3.00 × 10⁸ m/s. What is the frequency of the light wave?

f = v/l = (3.00 × 10⁸ m/s)/(4.55 × 10^{- 7} m) = 6.59 × 10¹⁴ Hz.

A wave on a string has a frequency of 440 Hz and a wavelength of 1.3 m. How fast does the wave travel?

v = lf = (1.3 m)(440 Hz) = 570 m/s.

A transverse wave on a string travels with a speed of 550 m/s and has a wavelength of 0.62 m and an amplitude of 0.50 cm. What is the maximum speed and the maximum acceleration of a point on the string?

The points on the string oscillate with the same frequency as the wave frequency. The maximum speed of points doing simple harmonic motion is

v_max = 2pfA = 2p(v/l) A = 2p(550 m/s)/(0.62 m)](0.50 × 10^-2 m) = 28 m/s.

The maximum acceleration is

a_max = (2pf)²A = 1.6 × 10⁵ m/s ^2.

A wire with a linear density of 2.5 × 10^{- 3} kg/m is under 35 N of tension. How fast would a wave travel on the wire?

Equation (16.2) gives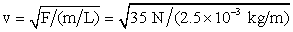

v = 120 m/s.

The waves traveling on a stretched wire travel with a speed of 180 m/s when the tension in the wire is 110 N. What is the linear density of the wire?

Equation (16.2) gives m/L = F/v² = (110 N)/(180 m/s)²

m/L = 3.4 × 10^{- 3} kg/m.

A wave has an amplitude of 0.70 mm, a wavelength of 5.5 m and travels with a speed of 150 m/s. Write an equation describing the wave.

Equation (16.3) describes a wave moving toward +x. In our case,

f = v/l = (150 m/s)/(5.5 m) = 27 Hz,

y = (0.70 mm) sin [(170 s^{- 1})t - (1.1 m^{- 1})x].

A wave is described by y = (1.0 cm) sin [(550 s^{- 1})t + (35 m^{- 1})x]. What are the amplitude, wavelength, frequency and velocity of the wave?

Compare the given equation with equation (16.4) for a wave traveling toward -x.

A = 1.0 cm, f = (550 s^{- 1})/2p = 88 Hz, l = 2p/(35 m^{- 1}) = 0.18 m

and the speed of the wave is

v = lf = 16 m/s.

The velocity is then

v = - 16 m/s.

A wave is described by y = (1.5 cm) sin [(150 m^{- 1})x - (760 s^{- 1})t]. How does this wave differ from one described by y' = (1.5 cm) sin[(760 s^{- 1})t - (150 m^-1)x]?

The first of the equations can be written

y = - (1.5 cm) sin [(760 s^{- 1})t - (150 m^{- 1})x]

due to the property of the sin function that sin (-q) = - sinq. The two waves are identical and both travel toward +x. The first is the negative of the second. That is, it is "flipped" over with respect to the second wave.

The speed of sound in a diatomic gas (g = 1.40) is measured at 27 °C to be 280 m/s. What is the molecular mass of the gas?

Using equation (16.5),

so that

m = gkT/v² = (1.4)(1.38 × 10^-23 J/K)(300 K)/(280 m/s)²

which yields, m = 7.4 × 10^-26 kg. The molecular mass is

(7.4 × 10^-23 g)(6.02 × 10²³ ) = 45 g.

10.

Brass has a Young's modulus of 9.0 × 10¹⁰ Pa and a density of 8470 kg/m³. How much time would it take for the sound to travel the length of a 5.5-m brass rod?

Using equation (16.7),

The time it takes to travel a distance of 5.5 m is therefore,

t = s/v = (5.5 m)/(3.3 × 10³ m/s) = 1.7 × 10^-3 s.

11.

At the bottom of a lake, a sound pulse is generated which is received by an observer 15.0 m above the surface of the lake in 0.100 s. Both the lake and air are at a temperature of 20.0 °C. How deep is the lake?

The distance traveled in the water is s_w = v_wt. The distance in air is s_a = v_a (0.100 s - t) = 15.0 m. Using v_a = 343 m/s we find t = 0.056 s. Therefore,

s_w = v_w t = (1482 m/s)(0.056 s) = 83 m.

12.

Two sounds have intensities of 2.0 × 10^-5 W/m² and 4.0 × 10^-8 W/m². What is the difference in the decibel levels of the two sounds?

The difference in intensity levels is

b = (10 dB) log (I₂/I₁) = (10 dB) log [(2.0 × 10^-5 W/m²)/(4.0 × 10^-8 W/m²)]

b = 27 dB.

13.

At a certain distance from a sound source, the intensity level is 75 dB. (a) What is the intensity of the sound in W/m²? (b) How much energy falls on a 5.0 m² area in 25 s?

(a)

b = (10 dB) log (I/I₀)

so that

I = I₀ × 10^{( b/(10 dB)} = (1.0 × 10^-12 W/m²) × 10^7.5 = 3.2 × 10^-5 W/m² .

(b)

P = IA = E/t

gives

E = IAt = (3.2 × 10^-5 W/m²)(5.0 m²)(25 s) = 4.0 × 10^-3 J.

14.

A listener triples his distance from a source that emits sound uniformly in all directions. By how many decibels does the sound intensity level change?

Using equation (16.9) we have

I₂/I₁ = (r₁/r₂)² = (r₁/3r₁)² = 1/9.

Therefore, the sound intensity changes by

b = (10 dB) log (I₂/I₁) = (10 dB) log (1/9) = - 9.5 dB.

15.

At 35 m from a uniformly radiating source of sound, the intensity level is 65 dB. At what distance from this source will its sound be just barely perceptible if absorption of sound by air is neglected?

Since

I₂/I₁ = (r₁/r₂)²

then

b = (10 dB) log (I₂/I₁) = (10 dB) log (r₁/r₂)² = (20 dB) log (r₁/r₂) = 65 dB.

Solving for r₁ yields

r₁ = r₂ × 10^{b/(20 dB )} = (35 m) × 10^{(65 dB)/(20 dB)} = (35 m) × 10^3.25 = 6.2 × 10⁴ m.

16.

A train whistle emits sound at a frequency of 555 Hz. A person standing next to the train track hears the whistle at a frequency of 488 Hz. What is the speed of the train? Is the train approaching or receding? Take the speed of sound to be 343 m/s.

Since the observed frequency decreases, this means the train is receding from the observer. Using

f_o = f_s [1/(1 + v_s/v)]

we get

v_s = v (f_s / f_o - 1) = (343 m/s){[(555 Hz)/(488 Hz)] - 1} = 47.1 m/s.

17.

A whistle of frequency 444 Hz rotates in a circle of radius 1.00 m with an angular speed of 25.0 rad/s. What is (a) the lowest frequency, and (b) the highest frequency heard by a listener a long distance away at rest with respect to the center of the circle?

To find the speed of the sound source use

v_s = rw = (1.00 m)(25.0 rad/s) = 25.0 m/s.

v_s/v = 0.0729.

(a)

For recession,

f_o = f_s [1/(1 + v_s/v)] = (444 Hz)[1/(1 + 0.0729)] = 414 Hz.

(b)

For approach,

f_o = f_s [1/(1 - v_s/v)] = (444 Hz)[1/(1 - 0.0729)] = 479 Hz.

18.

An ambulance travels down the highway at a speed of 120 km/h. Its siren emits sound at a frequency of 660 Hz. A passenger car traveling at 88 km/h is on the other side of the highway (i.e., it's traveling in the opposite direction as the ambulance). What is the frequency of the siren heard by a passenger in the car (a) as the car and ambulance are approaching each other, and (b) as the car and ambulance are receding from one another?

(a)

Both the source and the observer are approaching, so using equation (16.15) with a + sign in the numerator and a - sign in the denominator we have,

f_o = f_s (1 + v_o/v)/(1 - v_s/v) = (660 Hz)(1 + 0.0713)/(1 - 0.0971)

f_o = 780 Hz.

(b)

Now the source and observer are receding, so use a - sign in the numerator and a + sign in the denominator.We have f_o = f_s (1 - v_o/v)/(1 + v_s/v) = (660 Hz)(1 - 0.0713)/(1 + 0.0971) = 560 Hz.