In Figure 18.8 the grounding wire is removed first, followed by the rod, and the sphere is left with a positive charge. If the rod were removed first, followed by the grounding wire, would the sphere be left with a charge? Account for your answer.
A metallic object is given a positive charge by the process of induction, as illustrated in Figure 18.8. (a) Does the mass of the object increase, decrease, or remain the same? Why? (b) What happens to the mass of the object if it is given a negative charge by induction? Explain.
A rod made from insulating material carries a net charge, while a copper sphere is neutral. The rod and the sphere do not touch. Is it possible for the rod and the sphere to (a) attract one another and (b) repel one another? Explain.
On a dry day, just after washing your hair to remove natural oils and drying it thoroughly, run a plastic comb through it. Small bits of paper will be attracted to the comb. Explain why.
Blow up a balloon and rub it against your shirt a number of times. In so doing you give the balloon a net electric charge. Now touch the balloon to the ceiling. On being released, the balloon will remain stuck to the ceiling. Why?
A proton and an electron are held in place on the x axis. The proton is at x
=–d, while the electron is at x=+d. They are released simultaneously, and the only force that affects their motions is the electrostatic force of attraction that each applies to the other. Which particle reaches the origin first? Give your reasoning.
A particle is attached to a spring and is pushed so that the spring is compressed more and more. As a result, the spring exerts a greater and greater force on the particle. Similarly, a charged particle experiences a greater and greater force when pushed closer and closer to another particle that is fixed in position and has a charge of the same polarity. In spite of the similarity, the charged particle will not exhibit simple harmonic motion on being released, as will the particle on the spring. Explain why not.
Identical point charges are fixed to opposite corners of a square. Where does a third point charge experience the greater force, at one of the empty corners or at the center of the square? Account for your answer.
On a thin, nonconducting rod, positive charges are spread evenly, so that there is the same amount of charge per unit length at every point. On another identical rod, positive charges are spread evenly over only the left half, and the same amount of negative charges are spread evenly over the right half. For each rod, deduce the direction of the electric field at a point that is located directly above the midpoint of the rod. Give your reasoning.
There is an electric field at point P. A very small charge is placed at this point and experiences a force. Another very small charge is then placed at this point and experiences a force that differs in both magnitude and direction from that experienced by the first charge. How can these two different forces result from the single electric field that exists at point P?
Three point charges are fixed to the corners of a square, one to a corner, in such a way that the net electric field at the empty corner is zero. Do these charges all have (a) the same sign and (b) the same magnitude (but, possibly, different signs)? Justify your answers.
Review Conceptual Example 11 as an aid in answering this question. Suppose in Figure 18.21 that charges +q are placed on corners 1 and 3 of the rectangle, and charges –q are placed on corners 2 and 4. What is the net electric field at the center C of the rectangle?
In Figure 18.26 there is no place on the line through the charges where the electric field is zero, neither to the left of the positive charge, nor between the charges, nor to the right of the negative charge. Now, suppose the magnitude of the negative charge were greater than the magnitude of the positive charge. Is there any place on the line through the charges where the electric field is zero? Justify your answer.
Drawings I and II show two examples of electric field lines. Decide which of the following statements are true and which are false, defending your choice in each case. (a) In both I and II the electric field is the same everywhere. (b) As you move from left to right in each case, the electric field becomes stronger. (c) The electric field in I is the same everywhere but becomes stronger in II as you move from left to right. (d) The electric fields in both I and II could be created by negative charges located somewhere on the left and positive charges somewhere on the right. (e) Both I and II arise from a single positive point charge located somewhere on the left.
 |
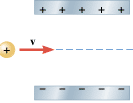
A positively charged particle is moving horizontally when it enters the region between the plates of a capacitor, as the drawing illustrates. (a) Draw the trajectory that the particle follows in moving through the capacitor. (b) When the particle is within the capacitor, which of the following four vectors, if any, are parallel to the electric field inside the capacitor: the particle’s displacement, its velocity, its linear momentum, its acceleration? For each vector explain why the vector is, or is not, parallel to the electric field of the capacitor.
Refer to Figure 18.27. Imagine a plane that is perpendicular to the line between the charges, midway between them, and is half into and half out of the paper. The electric flux through this plane is zero. Explain why.
Two charges, +q and –q, are inside a Gaussian surface. Since the net charge inside the Gaussian surface is zero, Gauss’ law states that the electric flux through the surface is also zero; that is, FE=0. Does the fact that FE=0 imply that the electric field E at any point on the Gaussian surface is also zero? Justify your answer.
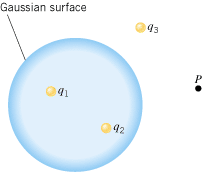
The drawing shows three charges, labeled q1, q2, and q3. A Gaussian surface is drawn around q1 and q2. (a) Which charges determine the electric flux through the Gaussian surface? (b) Which charges produce the electric field at the point P? Justify your answers.
A charge +q is placed inside a spherical Gaussian surface. The charge is not located at the center of the sphere. (a) Can Gauss’ law tell us exactly where the charge is located inside the sphere? Justify your answer. (b) Can Gauss’ law tell us about the magnitude of the electric flux through the Gaussian surface? Why?
|
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
