Coulomb's Law

18.5. Coulomb's Law

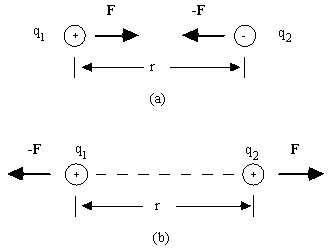
Consider two "point charges", q₁ and q₂, separated by a distance r, as shown in the diagram at the right. If the charges have unlike signs, as in part (a) of the diagram, each charge is attracted to the other by a force that is directed along the line between them; +F is the electric force exerted on charge 1 by charge 2 and -F is the electric force exerted on charge 2 by charge 1. If the charges have the same sign, as in (b), each charge is repelled by the other. The forces +F and -F form an action-reaction pair as predicted by Newton's third law.

The magnitude of the force (either attractive or repulsive) is given by Coulomb's law, i.e.,

(18.1)

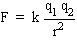where k is a constant of proportionality whose value in SI units is k = 8.99 x 10⁹ N·m²/C².

Example 2

What is the force between charges q₁ = + 1.0 mC and q₂ = - 2.0 mC which are separated by a distance of 2.0 m?

Equation (18.1) indicates the magnitude of the force is given by

Since the two charges have opposite signs, the force is one of attraction; q₁ will exert a force of 4.5 × 10^-3 N which attracts q₂. According to Newton's third law, q₂ will exert a force of 4.5 × 10^-3 N on q₁, which again is a force of attraction. Example 3 Force on a Point Charge due to Two or More Other Point Charges

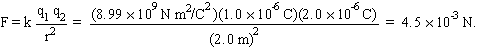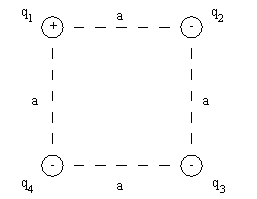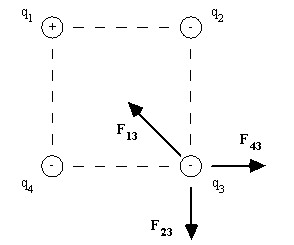
Consider four point charges arranged in the corners of a square, as shown in the diagram. Using,

q₁ = + 3.00 mC q₂ = - 1.20 mCq₃ = - 2.00 mC q₄ = - 1.20 mCa = 25.0 cm

find the net force acting on charge q₃ due to charges q₁, q₂, and q₄. Assume that all the point charges are fixed so that no motion occurs.

To find the net force acting on q₃, we need to find the vector sum of the forces acting on it. Note that q₃ will be repelled by q₂ and q₄, while q₃ will be attracted to q₁. If the force of charge q₁ acting on q₃ is F ₁₃, and the forces on q₃ due to charges 2 and 4 are F ₂₃ and F ₄₃, respectively, we can use the following diagram. We begin by calculating the magnitudes of the three forces acting on q₃. We will then use the rules of vector addition to find the desired resultant. The force exerted on the charge q₃ by the charge q₁ is, from Coulomb's law,

Similarly, for F₂₃ and F₄₃ we obtain,

We can now add forces F₁₃, F₂₃, and F₄₃ using the following vector diagram.

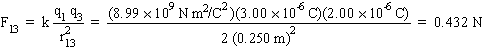Force

x component

y component

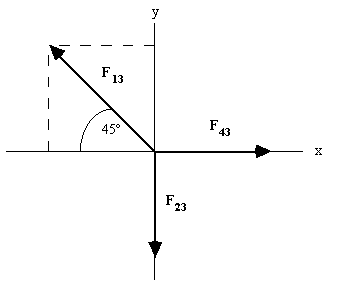
F₁₃

- (0.432 N) cos 45°= - 0.305 N

+ (0.432 N) sin 45°= + 0.305 N

F₂₃

= 0

= - 0.345 N

F₄₃

= + 0.345 N

= 0

= + 0.040 N

= - 0.040 N

The magnitude F of the resultant is given by

The angle q that the resultant force makes with the x axis is

where the negative angle means that the direction is clockwise with respect to the +x axis. In other words, the resultant force on q₃ is directed below the positive x axis.

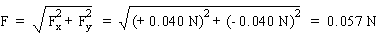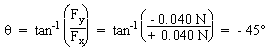So the general procedure for finding the force on a point charge due to two or more other point charges is to find the vector sum of the individual forces. The magnitudes of the forces are calculated from Coulomb's law. The directions of the forces are determined from the sign of each individual charge. That is, the force is either one of attraction or repulsion, depending on whether each pair of charges has unlike or like signs, respectively.