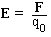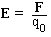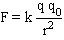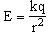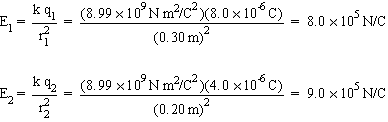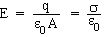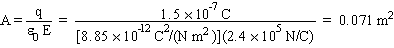18.6.
The Electric Field
A charge can experience an electrostatic force due to the presence of other charges in the environment. If a positive charge q0
is placed at a point in space, and if other charges are present, the charge q0
feels a force
F, which is the vector sum of the forces exerted on it by all the other charges present. We can define the electric field
E, that exists at this point, as the electrostatic force F divided by the test charge q0. That is,
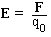 | (18.2) |  |
The electric field is a vector, and its direction is the same as the direction of the force F on a positive test charge. The SI unit of electric field is newtons per coulomb (N/C).
Consider the electrostatic force exerted by a point charge q on a test charge q0. The force is given by equation (18.1),
Using equation (18.2), we can see that the magnitude of the electric field due to a point charge can be written as
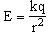 | (18.3) |  |
Example 4
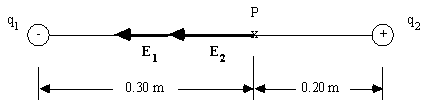
Two point charges, q1 = - 8.0 mC and q2 = + 4.0 mC, are separated by a distance of 0.50 m. Find the electric field (both magnitude and direction) at a point P on the line between the charges 0.20 m from q2.
We can see from the following diagram that the net electric field at point P is due to the combined effects of both charges. Note the directions of the fields
E
1
and
E
2; these are based on the fact that the direction of the field is the same as the direction of the force on a POSITIVE test charge.
Using equation (18.3) we have,
Since E1
and E2
are in the same direction, the total electric field is obtained by adding them together. Thus
| E = E1 + E2 = 8.0 × 105 N/C + 9.0 × 105 N/C = 1.7 × 106 N/C. |  |
The field E is directed to the left, or towards q1.
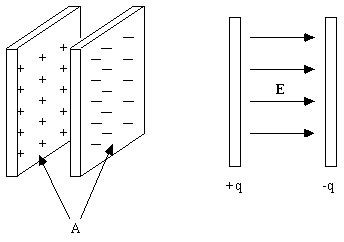
Now consider a parallel plate capacitor which consists of two parallel metal plates, each with area A. A charge +q is spread uniformly over one plate, while a charge -q is spread uniformly over the other plate. In the region between the plates and away from the edges, the electric field points from the positive plate toward the negative plate and has a magnitude of
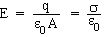 | (18.4) |  |
where
e
0
is the permittivity of free space and has a value of
e
0 = 8.85 × 10-12 C2/(N·m2), and
s = q/A is the surface charge density of the plates.
Example 5
The magnitude of the electric field between the plates of a parallel plate capacitor is 2.4 × 105 N/C. Each plate carries a charge whose magnitude is 0.15 mC. What is the area of the plates?
Using equation (18.4) and solving for A we obtain
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |