PRACTICE PROBLEMS

How many electrons must be removed from an electrically neutral silver dollar to give it a charge of +3.8 mC?

We know that q = Ne so,

N = q/e = (3.8 × 10-6 C)/(1.6 × 10-19 C)

N = 2.4 × 1013.

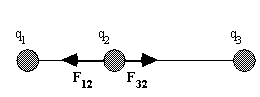
Three charges are located along a straight line, as shown below. What is the net electric force on charge q₂?

The forces on q₂ are shown in the diagram below.

Using Coulomb's law:

F12 = kq1q2/r12 2 = (8.99 × 109 N·m2/C2)(7.5 × 10-6 C)(4.0 × 10-6 C)/(0.40 m)2 = 1.7 N.

F32 = kq3q2/r32 2 = (8.99 × 109 N·m2/C2)(9.0 × 10-6 C)(4.0 × 10-6 C)/(0.60 m)2 = 0.90 N.

The net electric force on q₂ is therefore, F = F₁₂ - F₃₂ = 0.8 N to the left.

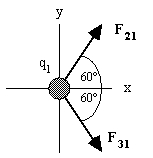
Three charges are located at the corners of an equilateral triangle, as shown below. What is the net electric force (magnitude and direction) acting on the top charge, q₁? Take d = 0.50 m.

The forces acting on q₁ are shown in the following diagram,

We have:

F21 = kq2q1/r21 2

F21 = (9.0 × 109 N·m2/C2)(5.0 mC)(3.5 mC)/(0.50 m)2

F21 = 0.63 N

Similarly,

F31 = kq3q1/r31 2 = 0.63 N.

So,

Fx = (F21)x + (F31)x

Fx = 2(0.63 N) cos 60° = 0.63 N.

Fy = (F21)y + (F31)y = 0.

Therefore, the net force acting on q₁ is 0.63 N in the +x direction.

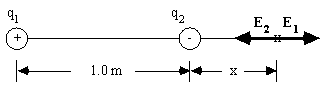
Two charges, q₁ = +5.0 mC and q₂ = -3.0 mC, are separated by a distance of 1.0 m. Find the spot along the line between the charges where the net electric field is zero.

Since q₁ and q₂ are of opposite sign, the electric field can not be zero in the region between the charges. Instead, E = 0 along the line joining the charges but away from the smaller charge, as in the figure below.

So, E₁ = kq₁/(1 + x)² = E₂ = kq₂/x²

or

q1x2 = q2(1 + x)2

5x2 = 3(1 + 2x + x2)

2x2 - 6x - 3 = 0.

Using the quadratic formula we find the solution to be x = 3.4 m.

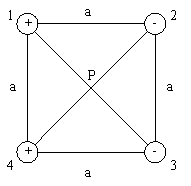
Four charges are arranged at the corners of a square, as shown below. Take a = 0.25 m. If all the charges have the same magnitude of 6.0 mC, what is the magnitude and direction of the electric field at P, the center of the square?

The total field at the center of the square is the vector sum of the fields due to each point charge.

Since each charge is equidistant from the center of the square, and since each charge has the same magnitude, the magnitudes of E₁ , E₂ , E₃, and E₄ are all the same. We have

E = kq/r2 = (8.99 × 109 N·m2/C2)(6.0 × 10-6 C)/(0.18 m)2

E = 1.7 × 106 N/C.

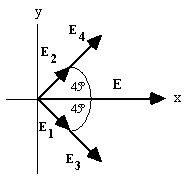
E_tot = E₁ + E₂ + E₃ + E₄ . From the diagram we see that (E_tot )_y = 0 and

(Etot )x = 4E cos 45° = 4.8 × 106 N/C.

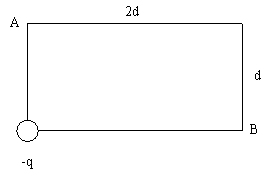
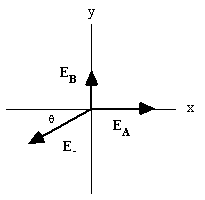
A negative charge -q is fixed to one corner of a rectangle, as in the drawing. What positive charge must be fixed to corner A and what positive charge must be fixed to corner B, so the total electric field at the remaining corner is zero? Express your answer in terms of q.

The field at the empty corner of the rectangle is the vector sum of the fields due to q_A, q_B, and q_-. We can see from the diagram that q = tan^-1 (d/2d) = 26.57°. Since the diagonal is of length d ,

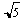E- = kq/(5d2),

Also,

EA = kqA/(4d2),

EB = kqB/d2,

(E-)x = EA, and (E-)y = EB.

Thus,

(E-)x = E- cos 26.57° = (kq cos 26.57°)/(5d2)

(E-)x = kqA/(4d2)

So,

qA = (4/5)q cos 26.57° = 0.716 q.

Now

(E-)y = E- sin 26.57° = (kq sin 26.57°)/(5d2)

(E-)y= kqB/d2

So,

qB = (1/5)q sin 26.57° = 0.0895 q.

Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved.
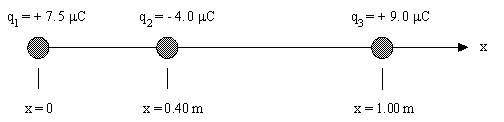
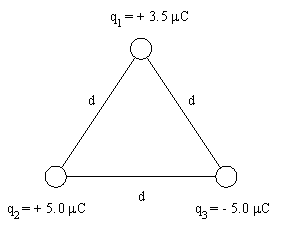
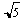