Appendix D. Exponents and Logarithms
Appendix A discusses powers of ten, such as 103, which means ten multiplied by itself three times, or 10![]() ×
×![]() 10
10![]() ×
×![]() 10. The three is referred to as an exponent. The use of exponents extends beyond powers of ten. In general, the term yn means the factor y is multiplied by itself n times. For example, y2, or y squared, is familiar and means y
10. The three is referred to as an exponent. The use of exponents extends beyond powers of ten. In general, the term yn means the factor y is multiplied by itself n times. For example, y2, or y squared, is familiar and means y![]() ×
×![]() y. Similarly, y5 means y
y. Similarly, y5 means y![]() ×
×![]() y
y![]() ×
×![]() y
y![]() ×
×![]() y
y![]() ×
×![]() y.
y.
The rules that govern algebraic manipulations of exponents are the same as those given in Appendix A (see Equations A-1, A-2, and A-3) for powers of ten:
 |
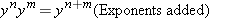 |
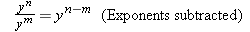 |
To the three rules above we add two more that are useful. One of these is
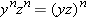 |
The following example helps to clarify the reasoning behind this rule:
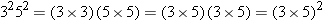 |
The other additional rule is
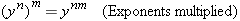 |
To see why this rule applies, consider the following example:
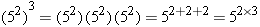 |
Roots, such as a square root or a cube root, can be represented with fractional exponents. For instance,
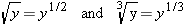 |
In general, the nth root of y is given by
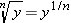 |
The rationale for Equation D-6 can be explained using the fact that (yn)m![]() =
=![]() ynm. For instance, the fifth root of y is the number that, when multiplied by itself five times, gives back y. As shown below, the term y1/5 satisfies this definition:
ynm. For instance, the fifth root of y is the number that, when multiplied by itself five times, gives back y. As shown below, the term y1/5 satisfies this definition:
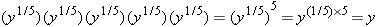 |
Logarithms are closely related to exponents. To see the connection between the two, note that it is possible to express any number y as another number B raised to the exponent x. In other words,
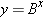 |
The exponent x is called the logarithm of the number y. The number B is called the base number. One of two choices for the base number is usually used. If B![]() =
=![]() 10, the logarithm is known as the common logarithm, for which the notation “log” applies:
10, the logarithm is known as the common logarithm, for which the notation “log” applies:
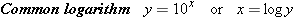 |
If B![]() =
=![]() e
e![]() =
=![]() 2.718…, the logarithm is referred to as the natural logarithm, and the notation “ln” is used:
2.718…, the logarithm is referred to as the natural logarithm, and the notation “ln” is used:
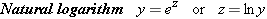 |
The two kinds of logarithms are related by
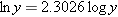 |
Both kinds of logarithms are often given on calculators.
The logarithm of the product or quotient of two numbers A and C can be obtained from the logarithms of the individual numbers according to the rules below. These rules are illustrated here for natural logarithms, but they are the same for any kind of logarithm.
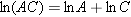 |
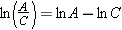 |
Thus, the logarithm of the product of two numbers is the sum of the individual logarithms, and the logarithm of the quotient of two numbers is the difference between the individual logarithms. Another useful rule concerns the logarithm of a number A raised to an exponent n:
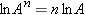 |
Rules D-11, D-12, and D-13 can be derived from the definition of the logarithm and the rules governing exponents.