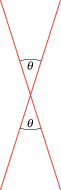
They are vertical angles (see Figure E1).
 |
| Figure E1 |
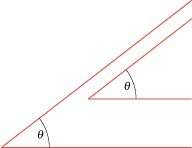
Their sides are parallel (see Figure E2).
 |
| Figure E2 |
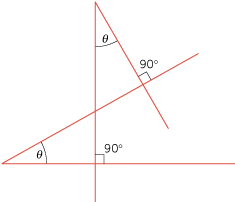
Their sides are mutually perpendicular (see Figure E3).
 |
| Figure E3 |
Appendix E. Geometry and Trigonometry
E.1 Geometry
ANGLES
Two angles are equal if
They are vertical angles (see Figure E1).
 |
| Figure E1 |
Their sides are parallel (see Figure E2).
 |
| Figure E2 |
Their sides are mutually perpendicular (see Figure E3).
 |
| Figure E3 |
TRIANGLES
The sum of the angles of any triangle is 180° (see Figure E4).
 |
| Figure E4 |
A right triangle has one angle that is 90°.
An isosceles triangle has two sides that are equal.
An equilateral triangle has three sides that are equal. Each angle of an equilateral triangle is 60°.
Two triangles are similar if two of their angles are equal (see Figure E5). The corresponding sides of similar triangles are proportional to each other:
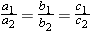 |
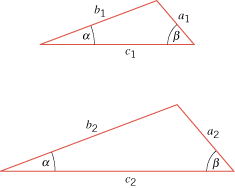 |
| Figure E5 |
Two similar triangles are congruent if they can be placed on top of one another to make an exact fit.
CIRCUMFERENCES, AREAS, AND VOLUMES OF SOME COMMON SHAPES
Triangle of base b and altitude h (see Figure E6):
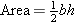 |
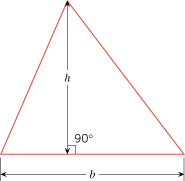 |
| Figure E6 |
Circle of radius r:
 |
Sphere of radius r:
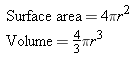 |
Right circular cylinder of radius r and height h (see Figure E7):
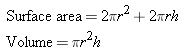 |
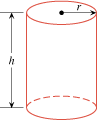 |
| Figure E7 |
E.2 Trigonometry
BASIC TRIGONOMETRIC FUNCTIONS
For a right triangle, the sine, cosine, and tangent of an angle q are defined as follows (see Figure E8):
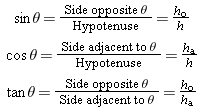 |
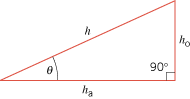 |
| Figure E8 |
The secant (sec q ), cosecant (csc q ), and cotangent (cot q ) of an angle q are defined as follows:
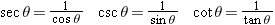 |
TRIANGLES AND TRIGONOMETRY
The Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides (see Figure E8):
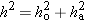 |
The law of cosines and the law of sines apply to any triangle, not just a right triangle, and they relate the angles and the lengths of the sides (see Figure E9):
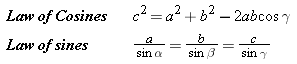 |
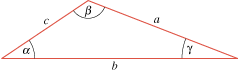 |
| Figure E9 |
OTHER TRIGONOMETRIC IDENTITIES
sin (–q )![]() =
=![]() –sin q
–sin q
cos (–q )![]() =
=![]() cos q
cos q
tan (–q )![]() =
=![]() –tan q
–tan q
(sin q )/(cos q )![]() =
=![]() tan q
tan q
sin2 q ![]() +
+![]() cos2 q
cos2 q ![]() =
=![]() 1
1
sin (a![]() ±
±![]() b)
b)![]() =
=![]() sin a cos b
sin a cos b![]() ±
±![]() cos a sin b
cos a sin b
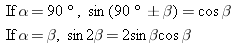 |
cos (a![]() ±
±![]() b)
b)![]() =
=![]() cos a cos b
cos a cos b 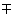 sin a sin b
sin a sin b
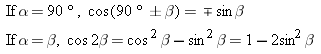 |