1.7.
The Components of a Vector
VECTOR COMPONENTS
Suppose a car moves along a straight line from start to finish in Figure 1.15, the corresponding displacement vector being r. The magnitude and direction of the vector r give the distance and direction traveled along the straight line. However, the car could also arrive at the finish point by first moving due east, turning through 90°, and then moving due north. This alternative path is shown in the drawing and is associated with the two displacement vectors x and y. The vectors x and y are called the x vector component and the y vector component of r.
 | | Figure 1.15
The displacement vector r and its vector components x and y. |
|
Vector components are very important in physics and have two basic features that are apparent in Figure 1.15. One is that the components add together to equal the original vector:
The components x and y, when added vectorially, convey exactly the same meaning as does the original vector r: they indicate how the finish point is displaced relative to the starting point. In general, the components of any vector can be used in place of the vector itself in any calculation where it is convenient to do so. The other feature of vector components that is apparent in Figure 1.15 is that x and y are not just any two vectors that add together to give the original vector r: they are perpendicular vectors. This perpendicularity is a valuable characteristic, as we will soon see.
Any type of vector may be expressed in terms of its components, in a way similar to that illustrated for the displacement vector in Figure 1.15. Figure 1.16 shows an arbitrary vector A and its vector components Ax and Ay. The components are drawn parallel to convenient x and y axes and are perpendicular. They add vectorially to equal the original vector A:
 | | Figure 1.16
An arbitrary vector A and its vector components A
x
and A
y
. |
|
There are times when a drawing such as Figure 1.16 is not the most convenient way to represent vector components, and Figure 1.17 presents an alternative method. The disadvantage of this alternative is that the tail-to-head arrangement of Ax and Ay is missing, an arrangement that is a nice reminder that Ax and Ay add together to equal A.
 | | Figure 1.17
This alternative way of drawing the vector A and its vector components is completely equivalent to that shown in Figure 1.16
|
|
The definition that follows summarizes the meaning of vector components:
The values calculated for vector components depend on the orientation of the vector relative to the axes used as a reference. Figure 1.18 illustrates this fact for a vector A by showing two sets of axes, one set being rotated clockwise relative to the other. With respect to the black axes, vector A has perpendicular vector components Ax and Ay; with respect to the colored rotated axes, vector A has different vector components  and
and  . The choice of which set of components to use is purely a matter of convenience.
. The choice of which set of components to use is purely a matter of convenience.
 | | Figure 1.18
The vector components of the vector depend on the orientation of the axes used as a reference. |
|
SCALAR COMPONENTS
It is often easier to work with the scalar components, Ax and Ay (note the italic symbols), rather than the vector components Ax and Ay. Scalar components are positive or negative numbers (with units) that are defined as follows. The component Ax has a magnitude that is equal to that of Ax and is given a positive sign if Ax points along the +x axis and a negative sign if Ax points along the –x axis. The component Ay is defined in a similar manner. The following table shows an example of vector and scalar components:
|
Vector Components
|
Scalar Components
|
Unit Vectors
| |
Ax = = 8 meters, directed along the +x axis 8 meters, directed along the +x axis
|
Ax = = +8 meters +8 meters
|
Ax = = (+8 meters) (+8 meters)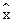
|
Ay = = 10 meters, directed along the –x axis 10 meters, directed along the –x axis
|
Ay = = –10 meters –10 meters
|
Ay = = (–10 meters) (–10 meters)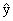
|
|
In this text, when we use the term “component,” we will be referring to a scalar component, unless otherwise indicated.
Another method of expressing vector components is to use unit vectors. A unit vector is a vector that has a magnitude of 1, but no dimensions. We will use a caret (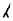 ) to distinguish it from other vectors. Thus,
) to distinguish it from other vectors. Thus,
| |
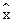 is a dimensionless unit vector of length l that points in the positive x direction, and is a dimensionless unit vector of length l that points in the positive x direction, and
|
| |
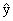 is a dimensionless unit vector of length l that points in the positive y direction. is a dimensionless unit vector of length l that points in the positive y direction.
|
These unit vectors are illustrated in Figure 1.19. With the aid of unit vectors, the vector components of an arbitrary vector A can be written as Ax =
= Ax
Ax 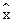 and Ay
and Ay =
= Ay
Ay 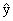 , where Ax and Ay are its scalar components (see the drawing and third column of the table above). The vector A is then written as A
, where Ax and Ay are its scalar components (see the drawing and third column of the table above). The vector A is then written as A =
= Ax
Ax 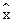
 +
+ Ay
Ay 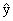
 | Figure 1.19
The dimensionless unit vectors 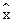 and and 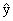 have magnitudes equal to 1, and they point in the +
x and +
y directions, respectively. Expressed in terms of unit vectors, the vector components of the vector A are A
x have magnitudes equal to 1, and they point in the +
x and +
y directions, respectively. Expressed in terms of unit vectors, the vector components of the vector A are A
x
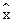 and A
y and A
y
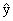 . . |
|
| Check Your Understanding 3 |
RESOLVING A VECTOR INTO ITS COMPONENTS
If the magnitude and direction of a vector are known, it is possible to find the components of the vector. The process of finding the components is called “resolving the vector into its components.” As Example 7 illustrates, this process can be carried out with the aid of trigonometry, because the two perpendicular vector components and the original vector form a right triangle.
| Example 7 Finding the Components of a Vector |
Since the vector components and the original vector form a right triangle, the Pythagorean theorem can be applied to check the validity of calculations such as those in Example 7. Thus, with the components obtained in Example 7, the theorem can be used to verify that the magnitude of the original vector is indeed 175 m, as given initially:
Problem solving insight
You can check to see whether the components of a vector are correct by substituting them into the Pythagorean theorem and verifying that the result is the magnitude of the original vector. |
|
It is possible for one of the components of a vector to be zero. This does not mean that the vector itself is zero, however. For a vector to be zero, every vector component must individually be zero. Thus, in two dimensions, saying that A =
= 0 is equivalent to saying that Ax
0 is equivalent to saying that Ax =
= 0 and Ay
0 and Ay =
= 0. Or, stated in terms of scalar components, if A
0. Or, stated in terms of scalar components, if A =
= 0, then Ax
0, then Ax =
= 0 and Ay
0 and Ay =
= 0.
0.
Two vectors are equal if, and only if, they have the same magnitude and direction. Thus, if one displacement vector points east and another points north, they are not equal, even if each has the same magnitude of 480 m. In terms of vector components, two vectors, A and B, are equal if, and only if, each vector component of one is equal to the corresponding vector component of the other. In two dimensions, if A =
= B, then Ax
B, then Ax =
= Bx and Ay
Bx and Ay =
= By. Alternatively, using scalar components, we write that Ax
By. Alternatively, using scalar components, we write that Ax =
= Bx and Ay
Bx and Ay =
= By.
By.
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |






 and
and  . The choice of which set of components to use is purely a matter of convenience.
. The choice of which set of components to use is purely a matter of convenience.
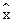
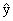
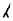 ) to distinguish it from other vectors. Thus,
) to distinguish it from other vectors. Thus,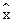 is a dimensionless unit vector of length l that points in the positive x direction, and
is a dimensionless unit vector of length l that points in the positive x direction, and
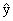 is a dimensionless unit vector of length l that points in the positive y direction.
is a dimensionless unit vector of length l that points in the positive y direction.
![]() =
=![]() Ax
Ax 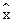 and Ay
and Ay![]() =
=![]() Ay
Ay 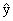 , where Ax and Ay are its scalar components (see the drawing and third column of the table above). The vector A is then written as A
, where Ax and Ay are its scalar components (see the drawing and third column of the table above). The vector A is then written as A![]() =
=![]() Ax
Ax 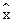
![]() +
+![]() Ay
Ay 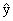


![]() =
=![]() 0 is equivalent to saying that Ax
0 is equivalent to saying that Ax![]() =
=![]() 0 and Ay
0 and Ay![]() =
=![]() 0. Or, stated in terms of scalar components, if A
0. Or, stated in terms of scalar components, if A![]() =
=![]() 0, then Ax
0, then Ax![]() =
=![]() 0 and Ay
0 and Ay![]() =
=![]() 0.
0.![]() =
=![]() B, then Ax
B, then Ax![]() =
=![]() Bx and Ay
Bx and Ay![]() =
=![]() By. Alternatively, using scalar components, we write that Ax
By. Alternatively, using scalar components, we write that Ax![]() =
=![]() Bx and Ay
Bx and Ay![]() =
=![]() By.
By.