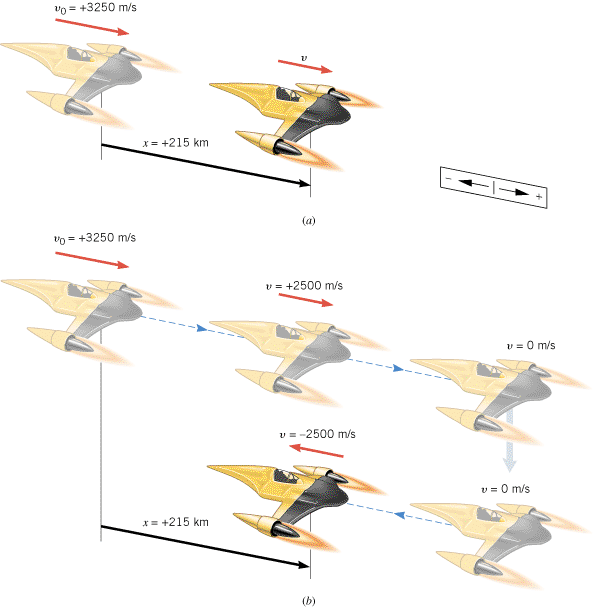
The spacecraft shown in Figure 2.14a is traveling with a velocity of +3250 m/s. Suddenly the retrorockets are fired, and the spacecraft begins to slow down with an acceleration whose magnitude is 10.0 m/s2. What is the velocity of the spacecraft when the displacement of the craft is +215 km, relative to the point where the retrorockets began firing?
 |
|
Reasoning
Since the spacecraft is slowing down, the acceleration must be opposite to the velocity. The velocity points to the right in the drawing, so the acceleration points to the left, in the negative direction; thus, a![]() =
=![]() –10.0 m/s2. The three known variables are listed as follows:
–10.0 m/s2. The three known variables are listed as follows:
Spacecraft Data
x
a
v
v0
t
+215 000 m
–10.0 m/s2
?
+3250 m/s
The final velocity v of the spacecraft can be calculated using Equation 2.9, since it contains the four pertinent variables.
Solution
From Equation 2.9 ( ), we find that
), we find that
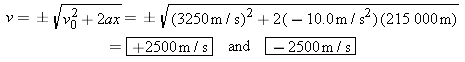 |