|
A motorcycle, starting from rest, has an acceleration of +2.6 m/s2. After the motorcycle has traveled a distance of 120 m, it slows down with an acceleration of –1.5 m/s2 until its velocity is +12 m/s (see Figure 2.15). What is the total displacement of the motorcycle?
 | | Figure 2.15
This motorcycle ride consists of two segments, each with a different acceleration. |
|
Reasoning
The total displacement is the sum of the displacements for the first (“speeding up”) and second (“slowing down”) segments. The displacement for the first segment is +120 m. The displacement for the second segment can be found if the initial velocity for this segment can be determined, since values for two other variables are already known (a = = –1.5 m/s2 and v –1.5 m/s2 and v = = +12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment. +12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment.
Solution
Recognizing that the motorcycle starts from rest (v0 = = 0 m/s), we can determine the final velocity v of the first segment from the given data: 0 m/s), we can determine the final velocity v of the first segment from the given data:
Segment 1 Data
|
x
|
a
|
v
|
v0
|
t
|
+120 m
|
+2.6 m/s2
|
?
|
0 m/s
|
|
From Equation 2.9 (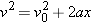 ), it follows that
Now we can use +25 m/s as the initial velocity for the second segment, along with the remaining data listed below: ), it follows that
Now we can use +25 m/s as the initial velocity for the second segment, along with the remaining data listed below:
Segment 2 Data
|
x
|
a
|
v
|
v0
|
t
|
?
|
–1.5 m/s2
|
+12 m/s
|
+25 m/s
|
|
The displacement for segment 2 can be obtained by solving 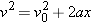 for x:
The total displacement of the motorcycle is for x:
The total displacement of the motorcycle is 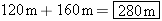 . .
 | | As this Harris hawk comes in for a landing on its trainer’s wrist, its velocity vector points in the same direction as its motion. However, since the hawk is slowing down, its acceleration vector points opposite to the velocity vector. (© Carl D. Walsh/Aurora & Quanta Productions) |
|
|

![]() =
=![]() –1.5 m/s2 and v
–1.5 m/s2 and v![]() =
=![]() +12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment.
+12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment.
![]() =
=![]() 0 m/s), we can determine the final velocity v of the first segment from the given data:
0 m/s), we can determine the final velocity v of the first segment from the given data:
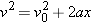 ), it follows that
), it follows that
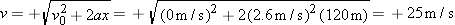
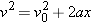 for x:
for x:

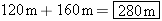 .
.
