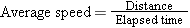
2.2.  Speed and Velocity

Average Speed

One of the most obvious features of an object in motion is how fast it is moving. If a car travels 200 meters in 10 seconds, we say its average speed is 20 meters per second, the average speed being the distance traveled divided by the time required to cover the distance:

(2.1)

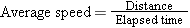Equation 2.1 indicates that the unit for average speed is the unit for distance divided by the unit for time, or meters per second (m/s) in SI units. Example 1 illustrates how the idea of average speed is used.

How far does a jogger run in 1.5 hours (5400 s) if his average speed is 2.22 m/s? Reasoning  The average speed of the jogger is the average distance per second that he travels. Thus, the distance covered by the jogger is equal to the average distance per second (his average speed) multiplied by the number of seconds (the elapsed time) that he runs. Solution To find the distance run, we rewrite Equation 2.1 as

Speed is a useful idea, because it indicates how fast an object is moving. However, speed does not reveal anything about the direction of the motion. To describe both how fast an object moves and the direction of its motion, we need the vector concept of velocity.

Average Velocity

CONCEPTS AT A GLANCE To define the velocity of an object, we will use two concepts that we have already encountered, displacement and time. The building of new concepts from more basic ones is a common theme in physics. In fact, the great strength of physics as a science is that it builds a coherent understanding of nature through the development of interrelated concepts. This development is so important that it is emphasized throughout this text by Concepts-at-a-Glance charts, such as that in Figure 2.2 These charts illustrate diagrammatically how useful ideas (e.g., velocity) emerge from more basic ones (e.g., displacement and time).

Figure 2.2  CONCEPTS AT A GLANCE The concepts of displacement and time are brought together to formulate the concept of velocity. The greater the velocity of these skiers, the greater is their displacement per unit time. (© Mark Junak/Stone/Getty Images)

Suppose that the initial position of the car in Figure 2.1 is x₀ when the time is t₀. A little later the car arrives at the final position x at the time t. The difference between these times is the time required for the car to travel between the two positions. We denote this difference by the shorthand notation Dt (read as “delta t”), where Dt represents the final time t minus the initial time t₀:

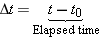Note that Dt is defined in a manner analogous to Dx, which is the final position minus the initial position (). Dividing the displacement Dx of the car by the elapsed time Dt gives the average velocity of the car. It is customary to denote the average value of a quantity by placing a horizontal bar above the symbol representing the quantity. The average velocity, then, is written as 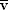, as specified in Equation 2.2:

DEFINITION OF AVERAGE VELOCITY

(2.2)  SI Unit of Average Velocity: meter per second (m/s)

Equation 2.2 indicates that the unit for average velocity is the unit for length divided by the unit for time, or meters per second (m/s) in SI units. Velocity can also be expressed in other units, such as kilometers per hour (km/h) or miles per hour (mi/h).

Average velocity is a vector that points in the same direction as the displacement in Equation 2.2. Figure 2.3 illustrates that the velocity of a car confined to move along a line can point either in one direction or in the opposite direction. As with displacement, we will use plus and minus signs to indicate the two possible directions. If the displacement points in the positive direction, the average velocity is positive. Conversely, if the displacement points in the negative direction, the average velocity is negative. Example 2 illustrates these features of average velocity.

Figure 2.3  In this time-lapse photo of traffic on the Los Angeles Freeway in California, the velocity of a car in the left lane (white headlights) is opposite to that of an adjacent car in the right lane (red taillights). (© Peter Essick/Aurora & Quanta Productions)

Andy Green in the car ThrustSSC set a world record of 341.1 m/s (763 mi/h) in 1997. The car was powered by two jet engines, and it was the first one officially to exceed the speed of sound. To establish such a record, the driver makes two runs through the course, one in each direction, to nullify wind effects. Figure 2.4a shows that the car first travels from left to right and covers a distance of 1609 m (1 mile) in a time of 4.740 s. Figure 2.4b shows that in the reverse direction, the car covers the same distance in 4.695 s. From these data, determine the average velocity for each run. Figure 2.4  The arrows in the box at the top of the drawing indicate the positive and negative directions for the displacements of the car, as explained in Example 2. Reasoning  Average velocity is defined as the displacement divided by the elapsed time. In using this definition we recognize that the displacement is not the same as the distance traveled. Displacement takes the direction of the motion into account, and distance does not. During both runs, the car covers the same distance of 1609 m. However, for the first run the displacement is Dx=+1609 m, while for the second it is Dx=–1609 m. The plus and minus signs are essential, because the first run is to the right, which is the positive direction, and the second run is in the opposite or negative direction. Solution According to Equation 2.2, the average velocities are In these answers the algebraic signs convey the directions of the velocity vectors. In particular, for Run 2 the minus sign indicates that the average velocity, like the displacement, points to the left in Figure 2.4b. The magnitudes of the velocities are 339.5 and 342.7 m/s. The average of these numbers is 341.1 m/s and is recorded in the record book.

A straight track is 1600 m in length. A runner begins at the starting line, runs due east for the full length of the track, turns around, and runs halfway back. The time for this run is five minutes. What is the runner’s average velocity, and what is his average speed? Background: Displacement, distance, velocity, and speed play roles in this problem. Displacement and distance are not the same thing; neither are velocity and speed. For similar questions (including calculational counterparts), consult Self-Assessment Test 2.1. This test is described at the end of Section 2.3.

Instantaneous Velocity

Suppose the magnitude of your average velocity for a long trip was 20 m/s. This value, being an average, does not convey any information about how fast you were moving at any instant during the trip. Surely there were times when your car traveled faster than 20 m/s and times when it traveled more slowly. The instantaneous velocity v of the car indicates how fast the car moves and the direction of the motion at each instant of time. The magnitude of the instantaneous velocity is called the instantaneous speed, and it is the number (with units) indicated by the speedometer.

The instantaneous velocity at any point during a trip can be obtained by measuring the time interval Dt for the car to travel a very small displacement Dx. We can then compute the average velocity over this interval. If the time Dt is small enough, the instantaneous velocity does not change much during the measurement. Then, the instantaneous velocity v at the point of interest is approximately equal to (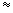) the average velocity computed over the interval, or (for sufficiently small Dt). In fact, in the limit that Dt becomes infinitesimally small, the instantaneous velocity and the average velocity become equal, so that

(2.3)

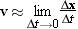The notation 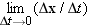means that the ratio Dx/Dt is defined by a limiting process in which smaller and smaller values of Dt are used, so small that they approach zero. As smaller values of Dt are used, Dx also becomes smaller. However, the ratio Dx/Dt does not become zero but, rather, approaches the value of the instantaneous velocity. For brevity, we will use the word velocity to mean “instantaneous velocity” and speed to mean “instantaneous speed.”

In a wide range of motions, the velocity changes from moment to moment. To describe the manner in which it changes, the concept of acceleration is needed.

Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved.