2.4.
Equations of Kinematics for Constant Acceleration
 CONCEPTS AT A GLANCE It is now possible to describe the motion of an object traveling with a constant acceleration along a straight line. To do so, we will use a set of equations known as the equations of kinematics for constant acceleration. These equations entail no new concepts, because they will be obtained by combining the familiar ideas of displacement, velocity, and acceleration, as the Concepts-at-a-Glance chart in Figure 2.10 shows. However, they will provide a very convenient way to determine certain aspects of the motion, such as the final position and velocity of a moving object.
CONCEPTS AT A GLANCE It is now possible to describe the motion of an object traveling with a constant acceleration along a straight line. To do so, we will use a set of equations known as the equations of kinematics for constant acceleration. These equations entail no new concepts, because they will be obtained by combining the familiar ideas of displacement, velocity, and acceleration, as the Concepts-at-a-Glance chart in Figure 2.10 shows. However, they will provide a very convenient way to determine certain aspects of the motion, such as the final position and velocity of a moving object.
|
| Figure 2.10
CONCEPTS AT A GLANCE The equations of kinematics for constant acceleration are obtained by combining the concepts of displacement, velocity, and acceleration. Whenever the drivers maintained a constant acceleration during the race, the equations of kinematics could have been used to calculate the displacement and velocity of these cars as a function of time. (© Mark Scott/Taxi/Getty Images) |
|
In discussing the equations of kinematics, it will be convenient to assume that the object is located at the origin x0 =
= 0 m when t0
0 m when t0 =
= 0 s. With this assumption, the displacement Dx
0 s. With this assumption, the displacement Dx =
= x
x –
– x0 becomes Dx
x0 becomes Dx =
= x. Furthermore, it is customary to dispense with the use of boldface symbols for the displacement, velocity, and acceleration vectors in the equations that follow. We will, however, continue to convey the directions of these vectors with plus or minus signs.
x. Furthermore, it is customary to dispense with the use of boldface symbols for the displacement, velocity, and acceleration vectors in the equations that follow. We will, however, continue to convey the directions of these vectors with plus or minus signs.
Consider an object that has an initial velocity of v0 at time t0 =
= 0 s and moves for a time t with a constant acceleration a. For a complete description of the motion, it is also necessary to know the final velocity and displacement at time t. The final velocity v can be obtained directly from Equation 2.4:
0 s and moves for a time t with a constant acceleration a. For a complete description of the motion, it is also necessary to know the final velocity and displacement at time t. The final velocity v can be obtained directly from Equation 2.4:
 | (2.4) |  |
The displacement x at time t can be obtained from Equation 2.2, if a value for the average velocity 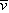 can be obtained. Considering the assumption that x0
can be obtained. Considering the assumption that x0 =
= 0 m at t0
0 m at t0 =
= 0 s, we have
0 s, we have
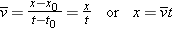 | (2.2) |  |
Because the acceleration is constant, the velocity increases at a constant rate. Thus, the average velocity 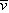 is midway between the initial and final velocities:
is midway between the initial and final velocities:
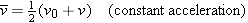 | (2.6) |  |
Equation 2.6, like Equation 2.4, applies only if the acceleration is constant and cannot be used when the acceleration is changing. The displacement at time t can now be determined as
 | (2.7) |  |
Notice in Equations 2.4 ( ) and 2.7 [
) and 2.7 [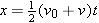 ] that there are five kinematic variables:
] that there are five kinematic variables:
| | 1. |
x = = displacement displacement
|
| | 2. |

|
| | 3. |
v = = final velocity at time t final velocity at time t
|
| | 4. |
v0 = = initial velocity at time t0 initial velocity at time t0 = = 0 s 0 s
|
| | 5. |
t = = time elapsed since t0 time elapsed since t0 = = 0 s 0 s
|
Each of the two equations contains four of these variables, so if three of them are known, the fourth variable can always be found. Example 5 illustrates how Equations 2.4 and 2.7 are used to describe the motion of an object.
| Example 5 The Displacement of a Speedboat |
 |
|
The speedboat in Figure 2.11 has a constant acceleration of +2.0 m/s2. If the initial velocity of the boat is +6.0 m/s, find its displacement after 8.0 seconds.
| | Figure 2.11
(a) An accelerating speedboat. (b) The boat’s displacement x can be determined if the boat’s acceleration, initial velocity, and time of travel are known. (© Onne van der Wal/Corbis Images) |
|
Reasoning
Numerical values for the three known variables are listed in the data table below. We wish to determine the displacement x of the speedboat, so it is an unknown variable. Therefore, we have placed a question mark in the displacement column of the data table.
Speedboat Data
|
x
|
a
|
v
|
v0
|
t
|
?
|
+2.0 m/s2
|
|
+6.0 m/s
|
8.0 s
|
We can use 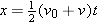 to find the displacement of the boat if a value for the final velocity v can be found. To find the final velocity, it is necessary to use the value given for the acceleration, because it tells us how the velocity changes, according to v to find the displacement of the boat if a value for the final velocity v can be found. To find the final velocity, it is necessary to use the value given for the acceleration, because it tells us how the velocity changes, according to v = = v0 v0 + + at. at.
Solution
The final velocity is
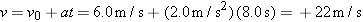 | (2.4) |  |
The displacement of the boat can now be obtained:
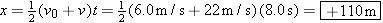 | (2.7) |  |
A calculator would give the answer as 112 m, but this number must be rounded to 110 m, since the data are accurate to only two significant figures.
|
 |
The solution to Example 5 involved two steps: finding the final velocity v and then calculating the displacement x. It would be helpful if we could find an equation that allows us to determine the displacement in a single step. Using Example 5 as a guide, we can obtain such an equation by substituting the final velocity v from Equation 2.4 (v =
= v0
v0 +
+ at) into Equation 2.7 [
at) into Equation 2.7 [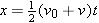 ]:
]:
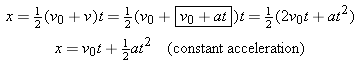 | (2.8) |  |
You can verify that Equation 2.8 gives the displacement of the speedboat directly without the intermediate step of determining the final velocity. The first term (v0t) on the right side of this equation represents the displacement that would result if the acceleration were zero and the velocity remained constant at its initial value of v0. The second term (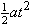 ) gives the additional displacement that arises because the velocity changes (a is not zero) to values that are different from its initial value. We now turn to another example of accelerated motion.
) gives the additional displacement that arises because the velocity changes (a is not zero) to values that are different from its initial value. We now turn to another example of accelerated motion.
 Concept Simulation 2.1 Concept Simulation 2.1 |
 |
This simulation compares motion at a constant velocity to motion at a constant acceleration. You can see the effect of setting the acceleration to different values. Related Homework: Problems 24, 26 |
|
 |
| Example 6 Catapulting a Jet |
Problem solving insight
“Implied data” are important. For instance, in Example 6 the phrase “starting from rest” means that the initial velocity is zero (v0 = = 0 m/s). 0 m/s). |
|
When a, v, and v0 are known, but the time t is not known, as in Example 6, it is possible to calculate the displacement x in a single step. Solving Equation 2.4 for the time [ ] and then substituting into Equation 2.7 [
] and then substituting into Equation 2.7 [ ] reveals that
] reveals that
Solving for v2 shows that
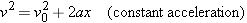 | (2.9) |  |
It is a straightforward exercise to verify that Equation 2.9 can be used to find the displacement of the jet in Example 6 without having to solve first for the time.
Table 2.1 presents a summary of the equations that we have been considering. These equations are called the equations of kinematics. Each equation contains four variables, as indicated by the check marks ( ) in the table. The next section shows how to apply the equations of kinematics.
) in the table. The next section shows how to apply the equations of kinematics.
| Table 2.1
Equations of Kinematics for Constant Acceleration |
|
|
|
Variables
| |
Equation Number
|
Equation
|
x
|
a
|
v
|
v0
|
t
| |
(2.4)
|
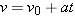
|
—
|
|
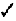
|
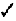
|
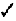
|
(2.7)
|
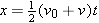
|
|
—
|
|
|
|
(2.8)
|
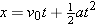
|
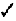
|
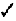
|
—
|
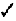
|
|
(2.9)
|

|
|
|
|
|
—
|
|
|
| Check Your Understanding 3 |
 |
|
A motorcycle starts from rest and has a constant acceleration. In a certain time interval, its displacement triples. In the same time interval, by what factor does its velocity increase?
Background:
When the acceleration is constant, the equations of kinematics given in Table 2.1 apply.
For similar questions (including calculational counterparts), consult Self-Assessment Test 2.2. This test is described at the end of Section 2.5.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() CONCEPTS AT A GLANCE It is now possible to describe the motion of an object traveling with a constant acceleration along a straight line. To do so, we will use a set of equations known as the equations of kinematics for constant acceleration. These equations entail no new concepts, because they will be obtained by combining the familiar ideas of displacement, velocity, and acceleration, as the Concepts-at-a-Glance chart in Figure 2.10 shows. However, they will provide a very convenient way to determine certain aspects of the motion, such as the final position and velocity of a moving object.
CONCEPTS AT A GLANCE It is now possible to describe the motion of an object traveling with a constant acceleration along a straight line. To do so, we will use a set of equations known as the equations of kinematics for constant acceleration. These equations entail no new concepts, because they will be obtained by combining the familiar ideas of displacement, velocity, and acceleration, as the Concepts-at-a-Glance chart in Figure 2.10 shows. However, they will provide a very convenient way to determine certain aspects of the motion, such as the final position and velocity of a moving object.![]() =
=![]() 0 m when t0
0 m when t0![]() =
=![]() 0 s. With this assumption, the displacement Dx
0 s. With this assumption, the displacement Dx![]() =
=![]() x
x![]() –
–![]() x0 becomes Dx
x0 becomes Dx![]() =
=![]() x. Furthermore, it is customary to dispense with the use of boldface symbols for the displacement, velocity, and acceleration vectors in the equations that follow. We will, however, continue to convey the directions of these vectors with plus or minus signs.
x. Furthermore, it is customary to dispense with the use of boldface symbols for the displacement, velocity, and acceleration vectors in the equations that follow. We will, however, continue to convey the directions of these vectors with plus or minus signs.![]() =
=![]() 0 s and moves for a time t with a constant acceleration a. For a complete description of the motion, it is also necessary to know the final velocity and displacement at time t. The final velocity v can be obtained directly from Equation 2.4:
0 s and moves for a time t with a constant acceleration a. For a complete description of the motion, it is also necessary to know the final velocity and displacement at time t. The final velocity v can be obtained directly from Equation 2.4:
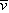 can be obtained. Considering the assumption that x0
can be obtained. Considering the assumption that x0![]() =
=![]() 0 m at t0
0 m at t0![]() =
=![]() 0 s, we have
0 s, we have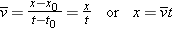
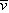 is midway between the initial and final velocities:
is midway between the initial and final velocities: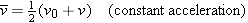

 ) and 2.7 [
) and 2.7 [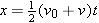 ] that there are five kinematic variables:
] that there are five kinematic variables:
![]() =
=![]() v0
v0![]() +
+![]() at) into Equation 2.7 [
at) into Equation 2.7 [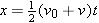 ]:
]: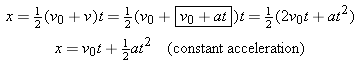
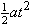 ) gives the additional displacement that arises because the velocity changes (a is not zero) to values that are different from its initial value. We now turn to another example of accelerated motion.
) gives the additional displacement that arises because the velocity changes (a is not zero) to values that are different from its initial value. We now turn to another example of accelerated motion. Concept Simulation 2.1
Concept Simulation 2.1 ] and then substituting into Equation 2.7 [
] and then substituting into Equation 2.7 [ ] reveals that
] reveals that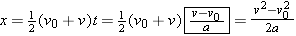
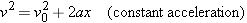
 ) in the table. The next section shows how to apply the equations of kinematics.
) in the table. The next section shows how to apply the equations of kinematics.