2.5.
Applications of the Equations of Kinematics
The equations of kinematics can be used for any moving object, as long as the acceleration of the object is constant. However, to avoid errors when using these equations, it helps to follow a few sensible guidelines and to be alert for a few situations that can arise during your calculations.
Decide at the start which directions are to be called positive (+) and negative (–) relative to a conveniently chosen coordinate origin. This decision is arbitrary, but important because displacement, velocity, and acceleration are vectors, and their directions must always be taken into account. In the examples that follow, the positive and negative directions will be shown in the drawings that accompany the problems. It does not matter which direction is chosen to be positive. However, once the choice is made, it should not be changed during the course of the calculation.
As you reason through a problem before attempting to solve it, be sure to interpret the terms “decelerating” or “deceleration” correctly, should they occur in the problem statement. These terms are the source of frequent confusion, and Conceptual Example 7 offers help in understanding them.
| Conceptual Example 7 Deceleration Versus Negative Acceleration |
 |
|
A car is traveling along a straight road and is decelerating. Does the car’s acceleration a necessarily have a negative value?
Reasoning and Solution We begin with the meaning of the term “decelerating,” which has nothing to do with whether the acceleration a is positive or negative. The term means only that the acceleration vector points opposite to the velocity vector and indicates that the moving object is slowing down. When a moving object slows down, its instantaneous speed (the magnitude of the instantaneous velocity) decreases. One possibility is that the velocity vector of the car points to the right, in the positive direction, as Figure 2.13a shows. The term “decelerating” implies that the acceleration vector points opposite, or to the left, which is the negative direction. Here, the value of the acceleration a would indeed be negative. However, there is another possibility. The car could be traveling to the left, as in Figure 2.13b. Now, since the velocity vector points to the left, the acceleration vector would point opposite or to the right, according to the meaning of the term “decelerating.” But right is the positive direction, so the acceleration a would have a positive value in Figure 2.13b. We see, then, that a decelerating object does not necessarily have a negative acceleration.
 | | Figure 2.13
When a car decelerates along a straight road, the acceleration vector points opposite to the velocity vector, as Conceptual Example 7 discusses. |
|
Related Homework:
Problems 20, 38
|
 |
Sometimes there are two possible answers to a kinematics problem, each answer corresponding to a different situation. Example 8 discusses one such case.
 Concept Simulation 2.2 Concept Simulation 2.2 |
 |
In this simulation you can see the motion of the spacecraft in Figure 2.14 and explore the effect of increasing or decreasing the magnitude of the deceleration. Related Homework: Conceptual Question 11, Problem 71 |
|
 |
| Example 8 An Accelerating Spacecraft |
 |
|
The spacecraft shown in Figure 2.14a is traveling with a velocity of +3250 m/s. Suddenly the retrorockets are fired, and the spacecraft begins to slow down with an acceleration whose magnitude is 10.0 m/s2. What is the velocity of the spacecraft when the displacement of the craft is +215 km, relative to the point where the retrorockets began firing?
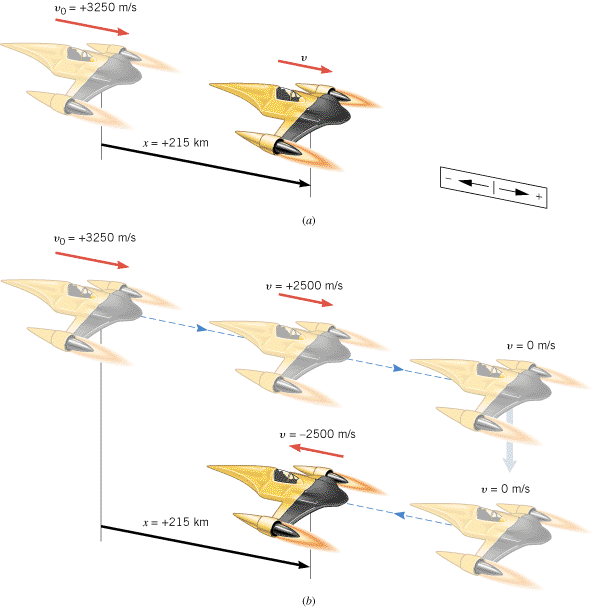 | | Figure 2.14
(a) Because of an acceleration of –10.0 m/s2, the spacecraft changes its velocity from v
0 to v. (b) Continued firing of the retrorockets changes the direction of the craft’s motion. |
|
Reasoning
Since the spacecraft is slowing down, the acceleration must be opposite to the velocity. The velocity points to the right in the drawing, so the acceleration points to the left, in the negative direction; thus, a = = –10.0 m/s2. The three known variables are listed as follows: –10.0 m/s2. The three known variables are listed as follows:
Spacecraft Data
|
x
|
a
|
v
|
v0
|
t
|
+215 000 m
|
–10.0 m/s2
|
?
|
+3250 m/s
|
|
The final velocity v of the spacecraft can be calculated using Equation 2.9, since it contains the four pertinent variables.
Solution
From Equation 2.9 ( ), we find that ), we find that
Both of these answers correspond to the same displacement (x = = +215 km), but each arises in a different part of the motion. The answer v +215 km), but each arises in a different part of the motion. The answer v = = +2500 m/s corresponds to the situation in Figure 2.14a, where the spacecraft has slowed to a speed of 2500 m/s, but is still traveling to the right. The answer v +2500 m/s corresponds to the situation in Figure 2.14a, where the spacecraft has slowed to a speed of 2500 m/s, but is still traveling to the right. The answer v = = –2500 m/s arises because the retrorockets eventually bring the spacecraft to a momentary halt and cause it to reverse its direction. Then it moves to the left, and its speed increases due to the continually firing rockets. After a time, the velocity of the craft becomes v –2500 m/s arises because the retrorockets eventually bring the spacecraft to a momentary halt and cause it to reverse its direction. Then it moves to the left, and its speed increases due to the continually firing rockets. After a time, the velocity of the craft becomes v = = –2500 m/s, giving rise to the situation in Figure 2.14b. In both parts of the drawing the spacecraft has the same displacement, but a greater travel time is required in part b compared to part a. –2500 m/s, giving rise to the situation in Figure 2.14b. In both parts of the drawing the spacecraft has the same displacement, but a greater travel time is required in part b compared to part a.
|
 |
The motion of two objects may be interrelated, so they share a common variable. The fact that the motions are interrelated is an important piece of information. In such cases, data for only two variables need be specified for each object. See Interactive LearningWare 2.2 for an example that illustrates this point.
 |
 Interactive LearningWare 2.2 Interactive LearningWare 2.2 | A bus has stopped to pick up riders. A woman is running at a constant velocity of +5.0 m/s in an attempt to catch the bus. When she is 11 m from the bus, it pulls away with a constant acceleration of +1.0 m/s2. From this point, how much time does it take her to reach the bus if she keeps running with the same velocity? Related Homework: Problems 56, 72, 76 |
|
 |
Often the motion of an object is divided into segments, each with a different acceleration. When solving such problems, it is important to realize that the final velocity for one segment is the initial velocity for the next segment, as Example 9 illustrates.
Problem solving insight
It is only when values are available for at least three of the five kinematic variables (x, a, v, v0, and t) that the equations in Table 2.1 can be used to determine the fourth and fifth variables. |
|
| Example 9 A Motorcycle Ride |
 |
|
A motorcycle, starting from rest, has an acceleration of +2.6 m/s2. After the motorcycle has traveled a distance of 120 m, it slows down with an acceleration of –1.5 m/s2 until its velocity is +12 m/s (see Figure 2.15). What is the total displacement of the motorcycle?
 | | Figure 2.15
This motorcycle ride consists of two segments, each with a different acceleration. |
|
Reasoning
The total displacement is the sum of the displacements for the first (“speeding up”) and second (“slowing down”) segments. The displacement for the first segment is +120 m. The displacement for the second segment can be found if the initial velocity for this segment can be determined, since values for two other variables are already known (a = = –1.5 m/s2 and v –1.5 m/s2 and v = = +12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment. +12 m/s). The initial velocity for the second segment can be determined, since it is the final velocity of the first segment.
Solution
Recognizing that the motorcycle starts from rest (v0 = = 0 m/s), we can determine the final velocity v of the first segment from the given data: 0 m/s), we can determine the final velocity v of the first segment from the given data:
Segment 1 Data
|
x
|
a
|
v
|
v0
|
t
|
+120 m
|
+2.6 m/s2
|
?
|
0 m/s
|
|
From Equation 2.9 (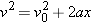 ), it follows that
Now we can use +25 m/s as the initial velocity for the second segment, along with the remaining data listed below: ), it follows that
Now we can use +25 m/s as the initial velocity for the second segment, along with the remaining data listed below:
Segment 2 Data
|
x
|
a
|
v
|
v0
|
t
|
?
|
–1.5 m/s2
|
+12 m/s
|
+25 m/s
|
|
The displacement for segment 2 can be obtained by solving 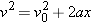 for x:
The total displacement of the motorcycle is for x:
The total displacement of the motorcycle is 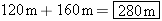 . .
 | | As this Harris hawk comes in for a landing on its trainer’s wrist, its velocity vector points in the same direction as its motion. However, since the hawk is slowing down, its acceleration vector points opposite to the velocity vector. (© Carl D. Walsh/Aurora & Quanta Productions) |
|
|
 |
Now that we have seen how the equations of kinematics are applied to various situations, it’s a good idea to summarize the reasoning strategy that has been used. This strategy, which is outlined below, will also be used when we consider freely falling bodies in Section 2.6 and two-dimensional motion in Chapter 3.
 |
| Applying the Equations of Kinematics | | | 1. | Make a drawing to represent the situation being studied. A drawing helps us to see what’s happening. | | | 2. | Decide which directions are to be called positive (+) and negative (–) relative to a conveniently chosen coordinate origin. Do not change your decision during the course of a calculation. | | | 3. | In an organized way, write down the values (with appropriate plus and minus signs) that are given for any of the five kinematic variables (x, a, v, v0, and t). Be on the alert for “implied data,” such as the phrase “starts from rest,” which means that the value of the initial velocity is v0 = = 0 m/s. The data summary boxes used in the examples in the text are a good way of keeping track of this information. In addition, identify the variables that you are being asked to determine. 0 m/s. The data summary boxes used in the examples in the text are a good way of keeping track of this information. In addition, identify the variables that you are being asked to determine. | | | 4. | Before attempting to solve a problem, verify that the given information contains values for at least three of the five kinematic variables. Once the three known variables are identified along with the desired unknown variable, the appropriate relation from Table 2.1 can be selected. Remember that the motion of two objects may be interrelated, so they may share a common variable. The fact that the motions are interrelated is an important piece of information. In such cases, data for only two variables need be specified for each object. | | | 5. | When the motion of an object is divided into segments, as in Example 9, remember that the final velocity of one segment is the initial velocity for the next segment. | | | 6. | Keep in mind that there may be two possible answers to a kinematics problem as, for instance, in Example 8. Try to visualize the different physical situations to which the answers correspond. |
|
|
 |
|
Test your understanding of the equations of kinematics for constant acceleration, which are discussed in Sections 2.4 and 2.5.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
 Concept Simulation 2.2
Concept Simulation 2.2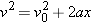 ), it follows that
), it follows that
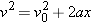 for x:
for x:
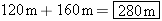 .
.