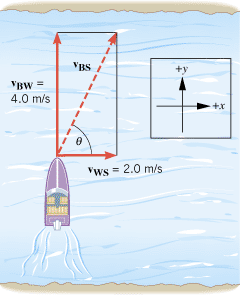
The engine of a boat drives it across a river that is 1800 m wide. The velocity v_BW of the boat relative to the water is 4.0 m/s, directed perpendicular to the current, as in Figure 3.18. The velocity v_WS of the water relative to the shore is 2.0 m/s. (a) What is the velocity v_BS of the boat relative to the shore? (b) How long does it take for the boat to cross the river?

Figure 3.18  The velocity of the boat relative to the shore is vBS. It is the vector sum of the velocity vBW of the boat relative to the water and the velocity vWS of the water relative to the shore:vBS=vBW+vWS.

Reasoning 

(a)	The velocity of the boat relative to the shore is vBS. It is the vector sum of the velocity vBW of the boat relative to the water and the velocity vWS of the water relative to the shore: vWS=vBW+vWS. Since vBW and vWS are both known, we can use this relation among the relative velocities, with the aid of trigonometry, to find the magnitude and directional angle of vBS.
(b)	The component of vBS that is parallel to the width of the river (see Figure 3.18) determines how fast the boat moves across the river; this parallel component is . The time for the boat to cross the river is equal to the width of the river divided by the magnitude of this velocity component.

Solution

(a)	Since the vectors vBW and vWS are perpendicular (see Figure 3.18), the magnitude of vBS can be determined by using the Pythagorean theorem: Thus, the boat moves at a speed of 4.5 m/s with respect to an observer on shore. The direction of the boat relative to the shore is given by the angle q  in the drawing:
(b)	The time t for the boat to cross the river is