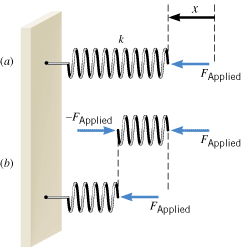
Figure 10.3a shows a 10-coil spring that has a spring constant k. If this spring is cut in half, so there are two 5-coil springs, what is the spring constant of each of the smaller springs?
 |
|
Reasoning and Solution It is tempting to say that each 5-coil spring has a spring constant of ½k or one-half the value for the 10-coil spring. However, the spring constant of each 5-coil spring is, in fact, 2k. Here’s the logic. When a force FApplied is applied to the spring, the displacement of the spring from its unstrained length is x, as Figure 10.3a illustrates. Now consider part b of the drawing, which shows the spring divided in half between the fifth and sixth coil (counting from the right). The spring is in equilibrium, so that the net force acting on the right half (coils 1-5) must be zero. Thus, as part b shows, a force of –FApplied must act on coil 5 in order to balance the force FApplied that acts on coil 1. It is the adjacent coil 6 that exerts the force –FApplied on coil 5, and Newton’s action-reaction law now comes into play. It tells us that coil 5, in response, exerts an oppositely directed force of equal magnitude on coil 6. In other words, the force FApplied is also exerted on the left half of the spring, as part b also indicates. As a result, the left half compresses by an amount that is one-half the displacement x experienced by the 10-coil spring. In summary, we have a 10-coil spring for which the force FApplied causes a displacement x and a 5-coil spring for which the same force causes a displacement ½x. We conclude, then, that the 5-coil spring must be twice as stiff as the 10-coil spring. When the 10-coil spring is cut in half, the spring constant of each resulting 5-coil spring is 2k. In general, the spring constant is inversely proportional to the number of coils in the spring, so shorter springs are stiffer springs, all other things being equal.
Related Homework: Problems 8, 16