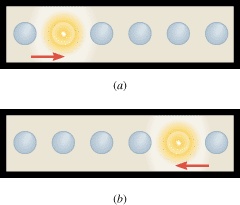
Over the entrance to a restaurant is mounted a strip of equally spaced light bulbs, as Figure 10.13a illustrates. Starting at the left end, each bulb turns on in sequence for one-half second. Thus, a lighted bulb appears to move from left to right. Once the apparent motion of a lighted bulb reaches the right side of the sign, the motion reverses. The lighted bulb then appears to move to the left, as part b of the drawing indicates. Thus, the lighted bulb appears to oscillate back and forth. Is the apparent motion simple harmonic motion?

Figure 10.13  The motion of a lighted bulb is from (a) left to right and then from (b) right to left.

Reasoning and Solution Since the bulbs are equally spaced and each bulb remains lit for the same amount of time, the apparent motion of a lighted bulb across the sign occurs at a constant speed. If the motion were simple harmonic motion, however, it would not have a constant speed (see Equation 10.7), because it would have zero speed at each end of the sign and increase to a maximum speed at the center of the sign. Therefore, although the apparent motion of a lighted bulb is oscillatory, it is not simple harmonic motion.