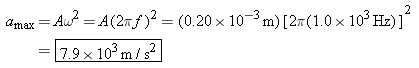|
The loudspeaker diaphragm in Figure 10.12 is vibrating at a frequency of f = = 1.0 kHz, and the amplitude of the motion is A 1.0 kHz, and the amplitude of the motion is A = = 0.20 mm. (a) What is the maximum acceleration of the diaphragm, and (b) where does this maximum acceleration occur? 0.20 mm. (a) What is the maximum acceleration of the diaphragm, and (b) where does this maximum acceleration occur?
Reasoning
The maximum acceleration amax of an object vibrating in simple harmonic motion is 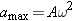 (w in rad/s), according to Equation 10.10. Equation 10.6 shows that the angular frequency w is related to the frequency f by (w in rad/s), according to Equation 10.10. Equation 10.6 shows that the angular frequency w is related to the frequency f by  . .
Problem solving insight
Do not confuse the vibrational frequency f with the angular frequency w. The value for f is in hertz (cycles per second). The value for v is in radians per second. The two are related by w = = 2p f. 2p f. |
|
Solution
| (a) |
Using Equations 10.10 and 10.6, we find that the maximum acceleration of the vibrating diaphragm is
This is an incredible acceleration, being more than 800 times the acceleration due to gravity, and the diaphragm must be built to withstand it.
| | (b) |
The maximum acceleration occurs when the force acting on the diaphragm is a maximum. The maximum force arises when the diaphragm is at the ends of its path, where the displacement is greatest. Thus, the maximum acceleration occurs at x = = +A and x +A and x = = –A in Figure 10.12. –A in Figure 10.12.
|
|
![]() =
=![]() 1.0 kHz, and the amplitude of the motion is A
1.0 kHz, and the amplitude of the motion is A![]() =
=![]() 0.20 mm. (a) What is the maximum acceleration of the diaphragm, and (b) where does this maximum acceleration occur?
0.20 mm. (a) What is the maximum acceleration of the diaphragm, and (b) where does this maximum acceleration occur?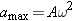 (w in rad/s), according to Equation 10.10. Equation 10.6 shows that the angular frequency w is related to the frequency f by
(w in rad/s), according to Equation 10.10. Equation 10.6 shows that the angular frequency w is related to the frequency f by  .
.