|
Figure 10.20a shows a box of mass m attached to a spring that has a force constant k. The box rests on a horizontal, frictionless surface. The spring is initially stretched to x = = A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x = = 0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion. 0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion.
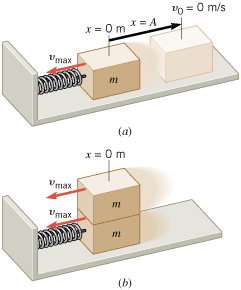 | Figure 10.20
(a) A box of mass m, starting from rest at x
 =
=
 A, undergoes simple harmonic motion about x
A, undergoes simple harmonic motion about x
 =
=
 0 m. (b) When x 0 m. (b) When x
 =
=
 0 m, a second box, with the same mass and speed, is attached. 0 m, a second box, with the same mass and speed, is attached. |
|
Reasoning and Solution
| (a) |
The maximum speed of an object in simple harmonic motion occurs when the object is passing through the point where the spring is unstrained (x = = 0 m), as in Figure 10.20b. Since the second box is attached at this point with the same speed, the maximum speed of the two-box system remains the same as that of the one-box system. 0 m), as in Figure 10.20b. Since the second box is attached at this point with the same speed, the maximum speed of the two-box system remains the same as that of the one-box system.
| | (b) |
At the same speed, the maximum kinetic energy of the two boxes is twice that of a single box, since the mass is twice as much. Subsequently, when the two boxes move to the left and compress the spring, their kinetic energy is converted into elastic potential energy. Since the two boxes have twice as much kinetic energy as one box alone, the two will have twice as much elastic potential energy when they come to a halt at the extreme left. Here, we are using the principle of conservation of mechanical energy, which applies since friction is absent. But the elastic potential energy is proportional to the amplitude squared (A2) of the motion, so the amplitude of the two-box system is greater than that of the one-box system by a factor of 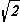 . .
| | (c) |
The angular frequency w of a simple harmonic oscillator is given by Equation 10.11 as  Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of  . .
|
Related Homework:
Conceptual Question 6
, Problem 32
|
![]() =
=![]() A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x
A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x![]() =
=![]() 0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion.
0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion.
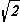 .
.
 Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of
Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of  .
.