|
A 0.20-kg ball is attached to a vertical spring, as in Figure 10.21. The spring constant of the spring is 28 N/m. The ball, supported initially so that the spring is neither stretched nor compressed, is released from rest. In the absence of air resistance, how far does the ball fall before being brought to a momentary stop by the spring?
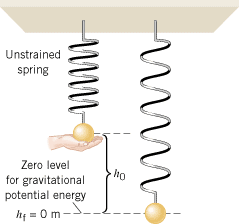 | | Figure 10.21
The ball is supported initially so that the spring is unstrained. After being released from rest, the ball falls through the distance h
0 before being momentarily stopped by the spring. |
|
Reasoning
Since air resistance is absent, only the conservative forces of gravity and the spring act on the ball. Therefore, the principle of conservation of mechanical energy applies:
The problem states that the final and initial translational speeds of the ball are zero: vf =v0=0 m/s. The ball and spring do not rotate, so the final and initial angular speeds are also zero: wf=w0=0 rad/s. As Figure 10.21 indicates, the initial height of the ball is h0, and the final height is hf=0 m. In addition, the spring is unstrained (x0=0 m) to begin with, and so it has no elastic potential energy initially. With these substitutions, the conservation of mechanical energy equation reduces to
This result shows that the initial gravitational potential energy (mgh0) is converted into elastic potential energy  . When the ball falls to its lowest point, its displacement is xf=–h0, where the minus sign indicates that the displacement is downward. Substituting this result into the equation above and solving for h0 yields h0=2mg/k.
Problem solving insight
When evaluating the total mechanical energy E, always include a potential energy term for every conservative force acting on the system. In Example 9 there are two such terms, gravitational and elastic. |
|
Solution
The distance that the ball falls before coming to a momentary halt is
|
