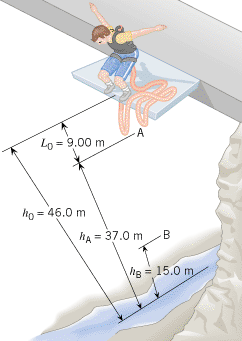
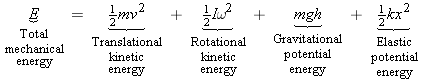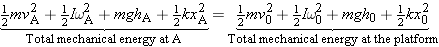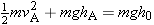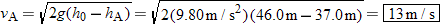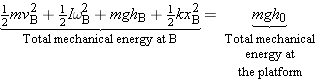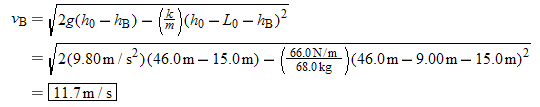Example 15 Bungee Jumping and the Conservation of Mechanical Energy

A 68.0-kg bungee jumper is standing on a tall platform (h₀=46.0 m), as indicated in Figure 10.36. The bungee cord has an unstrained length of L₀=9.00 m, and when stretched, behaves like an ideal spring with a spring constant of k=66.0 N/m. The jumper falls from rest, and the only forces acting on him are his weight and, for the latter part of the descent, the elastic force of the bungee cord. What is his speed (it is not zero) when he is at the following heights above the water (see the drawing): (a) h_A=37.0 m and (b) h_B=15.0 m?

A bungee jumper jumps from a height of h
0

46.0 m. The length of the unstrained bungee cord is L
0

9.00 m.

Figure 10.36 A bungee jumper jumps from a height of h ₀

46.0 m. The length of the unstrained bungee cord is L ₀

9.00 m.

Can we use the conservation of mechanical energy to find his speed at any point during the descent?

Yes. His weight and the elastic force of the bungee cord are the only forces acting on him and are conservative forces. Therefore, the total mechanical energy remains constant (is conserved) during his descent.

What types of energy does he have when he is standing on the platform?

Since he’s at rest, he has neither translational nor rotational kinetic energy. The bungee cord is not stretched, so there is no elastic potential energy. Relative to the water, however, he does have gravitational potential energy, since he is 46.0 m above it.

What types of energy does he have at point A?

Since he’s moving downward, he possesses translational kinetic energy. He is not rotating though, so his rotational kinetic energy is zero. Because the bungee cord is still not stretched at this point, there is no elastic potential energy. But he still has gravitational potential energy relative to the water, because he is 37.0 m above it.

What types of energy does he have at point B?

He has translational kinetic energy, because he’s still moving downward. He’s not rotating, so his rotational kinetic energy is zero. The bungee cord is stretched at this point, so there is elastic potential energy. He has gravitational potential energy, because he is still 15.0 m above the water.

Solution

(a)

The total mechanical energy is the sum of the kinetic and potential energies, as expressed in Equation 10.14:

The conservation of mechanical energy states that the total mechanical energy at point A is equal to that at the platform:

While standing on the platform, the jumper is at rest, so v₀

0 m/s and w₀

0 rad/s. The bungee cord is not stretched, so x₀

0 m. At point A, the jumper is not rotating, w_A

0 rad/s, and the bungee cord is still not stretched, x_A

0 m. With these substitutions, the conservation of mechanical energy becomes

Solving for the speed at point A yields

(b)

At point B the total mechanical energy is the same as it was on the platform, so

We set w_B

0 rad/s, since there is no rotational motion. Furthermore, the bungee cord stretches by an amount x_B

h₀ –

L₀ –

h_B (see the drawing). Therefore, we have