10.3.
Energy and Simple Harmonic Motion
We saw in Chapter 6 that an object above the surface of the earth has gravitational potential energy. Therefore, when the object is allowed to fall, like the hammer of the pile driver in Figure 6.13, it can do work. A spring also has potential energy when the spring is stretched or compressed, which we refer to as elastic potential energy. Because of elastic potential energy, a stretched or compressed spring can do work on an object that is attached to the spring. For instance, Figure 10.16 shows a door-closing unit that is often found on screen doors. When the door is opened, a spring inside the unit is compressed and has elastic potential energy. When the door is released, the compressed spring expands and does the work of closing the door.
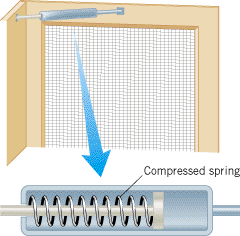 | | Figure 10.16
A door-closing unit. The elastic potential energy stored in the compressed spring is used to close the door. |
|
To find an expression for the elastic potential energy, we will determine the work done by the spring force on an object. Figure 10.17 shows an object attached to one end of a stretched spring. When the object is released, the spring contracts and pulls the object from its initial position x0 to its final position xf. The work W done by a constant force is given by Equation 6.1 as W =
= (F cos q )s, where F is the magnitude of the force, s is the magnitude of the displacement (s
(F cos q )s, where F is the magnitude of the force, s is the magnitude of the displacement (s =
= x0 –
x0 – xf), and q is the angle between the force and the displacement. The magnitude of the spring force is not constant, however. Equation 10.2 gives the spring force as F
xf), and q is the angle between the force and the displacement. The magnitude of the spring force is not constant, however. Equation 10.2 gives the spring force as F =
= –kx, and as the spring contracts, the magnitude of this force changes from kx0 to kxf. In using Equation 6.1 to determine the work, we can account for the changing magnitude by using an average magnitude
–kx, and as the spring contracts, the magnitude of this force changes from kx0 to kxf. In using Equation 6.1 to determine the work, we can account for the changing magnitude by using an average magnitude  in place of the constant magnitude F. Because the dependence of the spring force on x is linear, the magnitude of the average force is just one-half the sum of the initial and final values, or
in place of the constant magnitude F. Because the dependence of the spring force on x is linear, the magnitude of the average force is just one-half the sum of the initial and final values, or 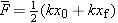 . The work Welastic done by the average spring force is, then,
. The work Welastic done by the average spring force is, then,
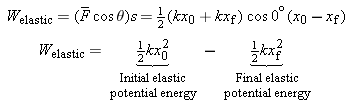 | (10.12) |  |
In the calculation above, q is 0°, since the spring force points to the left in Figure 10.17, which is the same direction as the displacement. Equation 10.12 indicates that the work done by the spring force is equal to the difference between the initial and final values of the quantity ½kx2. The quantity ½kx2 is analogous to the quantity mgh, which we identified in Section 6.3 as the gravitational potential energy. Here, we identify the quantity ½kx2 as the elastic potential energy. Equation 10.13 indicates that the elastic potential energy is a maximum for a fully stretched or compressed spring and zero for a spring that is neither stretched nor compressed (x =
= 0 m).
0 m).
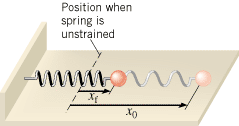 | | Figure 10.17
When the object is released, its displacement changes from an initial value of x0 to a final value of xf. |
|
| DEFINITION OF ELASTIC POTENTIAL ENERGY |
|
The elastic potential energy PEelastic is the energy that a spring has by virtue of being stretched or compressed. For an ideal spring that has a spring constant k and is stretched or compressed by an amount x relative to its unstrained length, the elastic potential energy is
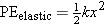 | (10.13) |  |
SI Unit of Elastic Potential Energy: joule (J)
|
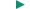 CONCEPTS AT A GLANCE The total mechanical energy E is a familiar idea that we originally defined to be the sum of the translational kinetic energy and the gravitational potential energy, as illustrated by the Concepts-at-a-Glance chart in Figure 6.15. Then, we included the rotational kinetic energy, as the chart in Figure 9.23 shows. We now expand the total mechanical energy to include the elastic potential energy, as the Concepts-at-a-Glance chart in Figure 10.18 indicates.
CONCEPTS AT A GLANCE The total mechanical energy E is a familiar idea that we originally defined to be the sum of the translational kinetic energy and the gravitational potential energy, as illustrated by the Concepts-at-a-Glance chart in Figure 6.15. Then, we included the rotational kinetic energy, as the chart in Figure 9.23 shows. We now expand the total mechanical energy to include the elastic potential energy, as the Concepts-at-a-Glance chart in Figure 10.18 indicates.
|
| Figure 10.18
CONCEPTS AT A GLANCE The elastic potential energy is added to other energies to give the total mechanical energy, which is conserved if Wnc, the net work done by external nonconservative forces, is zero. As this bungee jumper oscillates up and down at the end of the elastic cord, the total mechanical energy remains constant, to the extent that the nonconservative forces of friction and air resistance are negligible. (© Terje Rakke/Stone/Getty Images) |
|
In Equation 10.14 the elastic potential energy is included as part of the total mechanical energy:
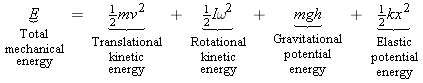 | (10.14) |  |
As Section 6.5 discusses, the total mechanical energy is conserved when external nonconservative forces (such as friction) do no net work; that is, when 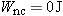 . Then, the final and initial values of E are the same: Ef
. Then, the final and initial values of E are the same: Ef =
= E0. The principle of conservation of total mechanical energy is the subject of the next example.
E0. The principle of conservation of total mechanical energy is the subject of the next example.
| Example 7 An Object on a Horizontal Spring |
 |
|
Figure 10.19 shows an object of mass m = = 0.200 kg that is vibrating on a horizontal frictionless table. The spring has a spring constant k 0.200 kg that is vibrating on a horizontal frictionless table. The spring has a spring constant k = = 545 N/m. It is stretched initially to x0 545 N/m. It is stretched initially to x0 = = 4.50 cm and then released from rest (see part A of the drawing). Determine the final translational speed vf of the object when the final displacement of the spring is (a) xf 4.50 cm and then released from rest (see part A of the drawing). Determine the final translational speed vf of the object when the final displacement of the spring is (a) xf = = 2.25 cm and (b) xf 2.25 cm and (b) xf = = 0 cm. 0 cm.
 | | Figure 10.19
The total mechanical energy of this system is entirely elastic potential energy (A), partly elastic potential energy and partly kinetic energy (B), and entirely kinetic energy (C). |
|
Reasoning
The conservation of mechanical energy indicates that, in the absence of friction (a nonconservative force), the final and initial total mechanical energies are the same (see Figure 10.18):
Since the object is moving on a horizontal table, the final and initial heights are the same: hf = = h0. The object is not rotating, so its angular speed is zero: wf h0. The object is not rotating, so its angular speed is zero: wf = = w0 w0 = = 0 rad/s. And, as the problem states, the initial translational speed of the object is zero, v0 0 rad/s. And, as the problem states, the initial translational speed of the object is zero, v0 = = 0 m/s. With these substitutions, the conservation-of-energy equation becomes
from which we can obtain vf: 0 m/s. With these substitutions, the conservation-of-energy equation becomes
from which we can obtain vf:
Solution
| (a) |
Since x0 = = 0.0450 m and xf 0.0450 m and xf = = 0.0225 m, the final translational speed is
The total mechanical energy at this point is partly translational kinetic energy ( 0.0225 m, the final translational speed is
The total mechanical energy at this point is partly translational kinetic energy ( ) and partly elastic potential energy ( ) and partly elastic potential energy ( ). The total mechanical energy E is the sum of these two energies: E ). The total mechanical energy E is the sum of these two energies: E = = 0.414 J + 0.414 J + 0.138 J 0.138 J = = 0.552 J. Because the total mechanical energy remains constant during the motion, this value equals the initial total mechanical energy when the object is stationary and the energy is entirely elastic potential energy ( 0.552 J. Because the total mechanical energy remains constant during the motion, this value equals the initial total mechanical energy when the object is stationary and the energy is entirely elastic potential energy ( ). ).
| | (b) |
When x0 = = 0.0450 m and xf 0.0450 m and xf = = 0 m, we have
Now the total mechanical energy is due entirely to the translational kinetic energy 0 m, we have
Now the total mechanical energy is due entirely to the translational kinetic energy  , since the elastic potential energy is zero. Note that the total mechanical energy is the same as it is in part (a). In the absence of friction, the simple harmonic motion of a spring converts the different types of energy between one form and another, the total always remaining the same. , since the elastic potential energy is zero. Note that the total mechanical energy is the same as it is in part (a). In the absence of friction, the simple harmonic motion of a spring converts the different types of energy between one form and another, the total always remaining the same.
|
|
 |
Conceptual Example 8 takes advantage of energy conservation to illustrate what happens to the maximum speed, amplitude, and angular frequency of a simple harmonic oscillator when its mass is changed suddenly at a certain point in the motion.
| Conceptual Example 8 Changing the Mass of a Simple Harmonic Oscillator |
 |
|
Figure 10.20a shows a box of mass m attached to a spring that has a force constant k. The box rests on a horizontal, frictionless surface. The spring is initially stretched to x = = A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x A and then released from rest. The box then executes simple harmonic motion that is characterized by a maximum speed vmax, an amplitude A, and an angular frequency w. When the box is passing through the point where the spring is unstrained (x = = 0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion. 0 m), a second box of the same mass m and speed vmax is attached to it, as in part b of the drawing. Discuss what happens to (a) the maximum speed, (b) the amplitude, and (c) the angular frequency of the subsequent simple harmonic motion.
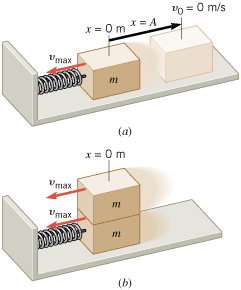 | Figure 10.20
(a) A box of mass m, starting from rest at x
 =
=
 A, undergoes simple harmonic motion about x
A, undergoes simple harmonic motion about x
 =
=
 0 m. (b) When x 0 m. (b) When x
 =
=
 0 m, a second box, with the same mass and speed, is attached. 0 m, a second box, with the same mass and speed, is attached. |
|
Reasoning and Solution
| (a) |
The maximum speed of an object in simple harmonic motion occurs when the object is passing through the point where the spring is unstrained (x = = 0 m), as in Figure 10.20b. Since the second box is attached at this point with the same speed, the maximum speed of the two-box system remains the same as that of the one-box system. 0 m), as in Figure 10.20b. Since the second box is attached at this point with the same speed, the maximum speed of the two-box system remains the same as that of the one-box system.
| | (b) |
At the same speed, the maximum kinetic energy of the two boxes is twice that of a single box, since the mass is twice as much. Subsequently, when the two boxes move to the left and compress the spring, their kinetic energy is converted into elastic potential energy. Since the two boxes have twice as much kinetic energy as one box alone, the two will have twice as much elastic potential energy when they come to a halt at the extreme left. Here, we are using the principle of conservation of mechanical energy, which applies since friction is absent. But the elastic potential energy is proportional to the amplitude squared (A2) of the motion, so the amplitude of the two-box system is greater than that of the one-box system by a factor of 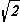 . .
| | (c) |
The angular frequency w of a simple harmonic oscillator is given by Equation 10.11 as  Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of Since the mass of the two-box system is twice that of the one-box system, the angular frequency of the two-box system is smaller than that of the one-box system by a factor of  . .
|
Related Homework:
Conceptual Question 6
, Problem 32
|
 |
In the previous two examples, gravitational potential energy plays no role because the spring is horizontal. The next example illustrates that gravitational potential energy must be taken into account when a spring is oriented vertically.
| Example 9 A Falling Ball on a Vertical Spring |
 |
|
A 0.20-kg ball is attached to a vertical spring, as in Figure 10.21. The spring constant of the spring is 28 N/m. The ball, supported initially so that the spring is neither stretched nor compressed, is released from rest. In the absence of air resistance, how far does the ball fall before being brought to a momentary stop by the spring?
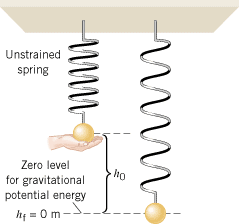 | | Figure 10.21
The ball is supported initially so that the spring is unstrained. After being released from rest, the ball falls through the distance h
0 before being momentarily stopped by the spring. |
|
Reasoning
Since air resistance is absent, only the conservative forces of gravity and the spring act on the ball. Therefore, the principle of conservation of mechanical energy applies:
The problem states that the final and initial translational speeds of the ball are zero: vf = = v0 v0 = = 0 m/s. The ball and spring do not rotate, so the final and initial angular speeds are also zero: wf 0 m/s. The ball and spring do not rotate, so the final and initial angular speeds are also zero: wf = = w0 w0 = = 0 rad/s. As Figure 10.21 indicates, the initial height of the ball is h0, and the final height is hf 0 rad/s. As Figure 10.21 indicates, the initial height of the ball is h0, and the final height is hf = = 0 m. In addition, the spring is unstrained (x0 0 m. In addition, the spring is unstrained (x0 = = 0 m) to begin with, and so it has no elastic potential energy initially. With these substitutions, the conservation of mechanical energy equation reduces to
This result shows that the initial gravitational potential energy (mgh0) is converted into elastic potential energy 0 m) to begin with, and so it has no elastic potential energy initially. With these substitutions, the conservation of mechanical energy equation reduces to
This result shows that the initial gravitational potential energy (mgh0) is converted into elastic potential energy  . When the ball falls to its lowest point, its displacement is xf . When the ball falls to its lowest point, its displacement is xf = = –h0, where the minus sign indicates that the displacement is downward. Substituting this result into the equation above and solving for h0 yields h0 –h0, where the minus sign indicates that the displacement is downward. Substituting this result into the equation above and solving for h0 yields h0 = = 2mg/k. 2mg/k.
Problem solving insight
When evaluating the total mechanical energy E, always include a potential energy term for every conservative force acting on the system. In Example 9 there are two such terms, gravitational and elastic. |
|
Solution
The distance that the ball falls before coming to a momentary halt is
|
 |
 Concept Simulation 10.1 Concept Simulation 10.1 |
 |
In this simulation you can control the initial velocity and mass of an object on a vertical spring. As the object oscillates, its vertical position and velocity are plotted as a function of time. You can also choose to display any or all of the following energies as a function of time: kinetic energy, gravitational potential energy, elastic potential energy, and total mechanical energy. Related Homework: Problem 25 |
|
 |
| Check Your Understanding 3 |
 |
|
A block is attached to the end of a horizontal ideal spring and rests on a frictionless surface. The block is pulled so that the spring stretches relative to its unstrained length. In each of the following three cases, the spring is stretched initially by the same amount, but the block is given different initial speeds. Rank the amplitudes of the resulting simple harmonic motion in decreasing order (largest first). (a) The block is released from rest. (b) The block is given an initial speed v0. (c) The block is given an initial speed v0/2.
Background:
Here, the pertinent themes are elastic potential energy, kinetic energy, energy conservation, and the amplitude of simple harmonic motion.
For similar questions (including calculational counterparts), consult Self-Assessment Test 10.2. This test is described at the end of Section 10.8.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |


![]() =
=![]() (F cos q )s, where F is the magnitude of the force, s is the magnitude of the displacement (s
(F cos q )s, where F is the magnitude of the force, s is the magnitude of the displacement (s![]() =
=![]() x0 –
x0 –![]() xf), and q is the angle between the force and the displacement. The magnitude of the spring force is not constant, however. Equation 10.2 gives the spring force as F
xf), and q is the angle between the force and the displacement. The magnitude of the spring force is not constant, however. Equation 10.2 gives the spring force as F![]() =
=![]() –kx, and as the spring contracts, the magnitude of this force changes from kx0 to kxf. In using Equation 6.1 to determine the work, we can account for the changing magnitude by using an average magnitude
–kx, and as the spring contracts, the magnitude of this force changes from kx0 to kxf. In using Equation 6.1 to determine the work, we can account for the changing magnitude by using an average magnitude  in place of the constant magnitude F. Because the dependence of the spring force on x is linear, the magnitude of the average force is just one-half the sum of the initial and final values, or
in place of the constant magnitude F. Because the dependence of the spring force on x is linear, the magnitude of the average force is just one-half the sum of the initial and final values, or 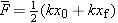 . The work Welastic done by the average spring force is, then,
. The work Welastic done by the average spring force is, then,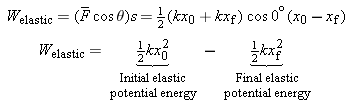
![]() =
=![]() 0 m).
0 m).
![]() CONCEPTS AT A GLANCE The total mechanical energy E is a familiar idea that we originally defined to be the sum of the translational kinetic energy and the gravitational potential energy, as illustrated by the Concepts-at-a-Glance chart in Figure 6.15. Then, we included the rotational kinetic energy, as the chart in Figure 9.23 shows. We now expand the total mechanical energy to include the elastic potential energy, as the Concepts-at-a-Glance chart in Figure 10.18 indicates.
CONCEPTS AT A GLANCE The total mechanical energy E is a familiar idea that we originally defined to be the sum of the translational kinetic energy and the gravitational potential energy, as illustrated by the Concepts-at-a-Glance chart in Figure 6.15. Then, we included the rotational kinetic energy, as the chart in Figure 9.23 shows. We now expand the total mechanical energy to include the elastic potential energy, as the Concepts-at-a-Glance chart in Figure 10.18 indicates.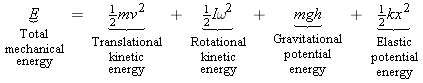
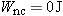 . Then, the final and initial values of E are the same: Ef
. Then, the final and initial values of E are the same: Ef![]() =
=![]() E0. The principle of conservation of total mechanical energy is the subject of the next example.
E0. The principle of conservation of total mechanical energy is the subject of the next example. Concept Simulation 10.1
Concept Simulation 10.1